Dans la foulée du scandale Bre-X, la plupart des pays importants sur le plan minier ont adopté des règles plus strictes concernant la divulgation des ressources et réserves. Le tableau suivant présente les principales réglementations :
| Pays | Réglementation |
|---|---|
| Canada | Règlement NI 43-101 |
| Australie | JORC Code |
| Afrique du Sud | SAMREC |
| Royaume-Uni | IMM |
| États-Unis | SME |
Principales réglementations sur la divulgation des ressources et réserves minérales.
Une des causes importantes à l’origine du scandale Bre-X a été l’altération frauduleuse des échantillons de carottes par l’ajout de poussière d’or. Afin d’éviter qu’une telle situation ne se reproduise sans être détectée, toutes les règlementations mentionnées dans le tableau ci-dessus incluent des recommandations précises quant au contrôle et à l’assurance qualité (QA/QC).
Dans le cas particulier du règlement NI 43-101 au Canada, le QA/QC constitue un des chapitres essentiels du rapport technique. Ce chapitre doit décrire en détail toutes les procédures utilisées pour assurer l’intégrité et la qualité des échantillons récoltés, incluant notamment :
les méthodes d’échantillonnage ;
les procédures d’entreposage ;
les systèmes de sécurité et de protection des accès (ex. : alarmes) ;
les outils et méthodes de contrôle utilisés pour détecter d’éventuelles irrégularités ou fraudes.
Définitions¶
On distingue quatre types principaux de contrôles de qualité (QA/QC) :
Analyse par un tiers (umpire assaying) : Le rejet[1] (ou la pulpe[2]) est envoyé à un second laboratoire pour une analyse indépendante. Cela permet de détecter un problème potentiel de précision ou de justesse du laboratoire principal.
Duplicatas : Le même laboratoire refait l’analyse à partir du rejet, idéalement à l’aveugle. Cela permet d’évaluer la précision des analyses. L’analyse par un tiers peut être considérée comme un duplicata externe.
Blancs : Une roche stérile est introduite dans les envois au laboratoire pour analyse. Cela permet de détecter une éventuelle contamination au sein du laboratoire.
Échantillons de référence (standards) : Des échantillons de référence ayant une teneur connue (avec un écart-type certifié) sont fournis par des entreprises spécialisées. Ils sont insérés entre deux échantillons réels. Cela permet de vérifier la justesse des analyses effectuées.
Exemple 1) Projet Windfall - Osiko¶
Voici un résumé des information pouvant être tiré du rapport technique NI-43-101 du Projet Windfall - Osiko daté de 2022.
Blancs constitués de gravier calcaire stérile.
Standards : identifiant effacé avant insertion dans le sac pour éviter toute reconnaissance au labo.
Introduction systématique de blancs et de matériaux de référence certifiés (standards) au fil de l’échantillonnage.
Utilisation d’étiquettes numérotées en triplicata : une dans le sac, une dans la boîte, une conservée dans le carnet.
Des standards sont insérés à une fréquence d’un tous les 20 échantillons afin de surveiller la justesse (accuracy) et la précision (precision) des résultats analytiques.
96,858 blancs, 87,029 standards, et 5,922 duplicatas
Blancs¶
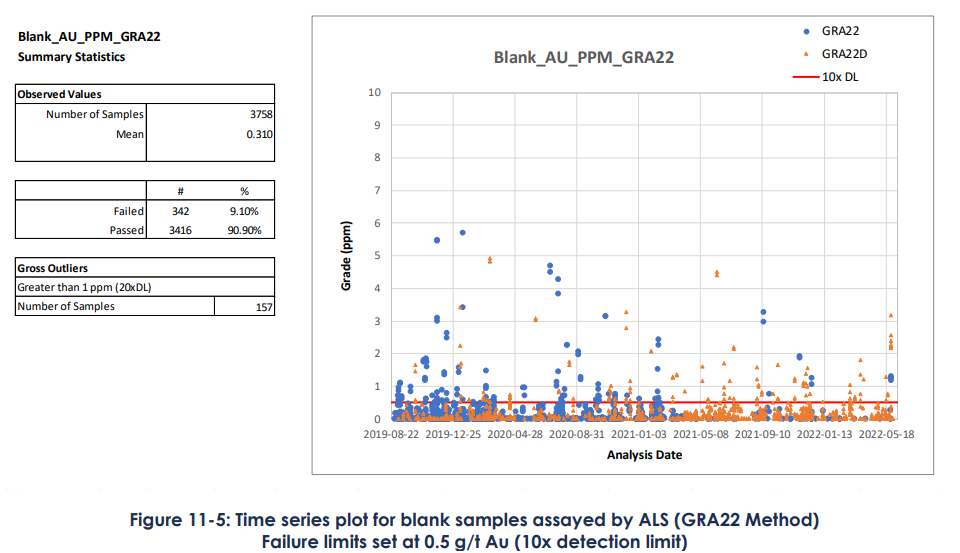
La Fig. 1 présente les résultats d’analyse des blancs du projet Windfall. La manière traditionnelle de présenter ces résultats est sous forme de série temporelle, où l’on montre les analyses au fur et à mesure de leur obtention.
On constate que les teneurs analysées sont, dans 90 % des cas, inférieures à dix fois la limite de détection (detection limit - DL). La personne qualifiée a jugé acceptable que 10 % des analyses dépassent ce seuil.
Duplicatas¶
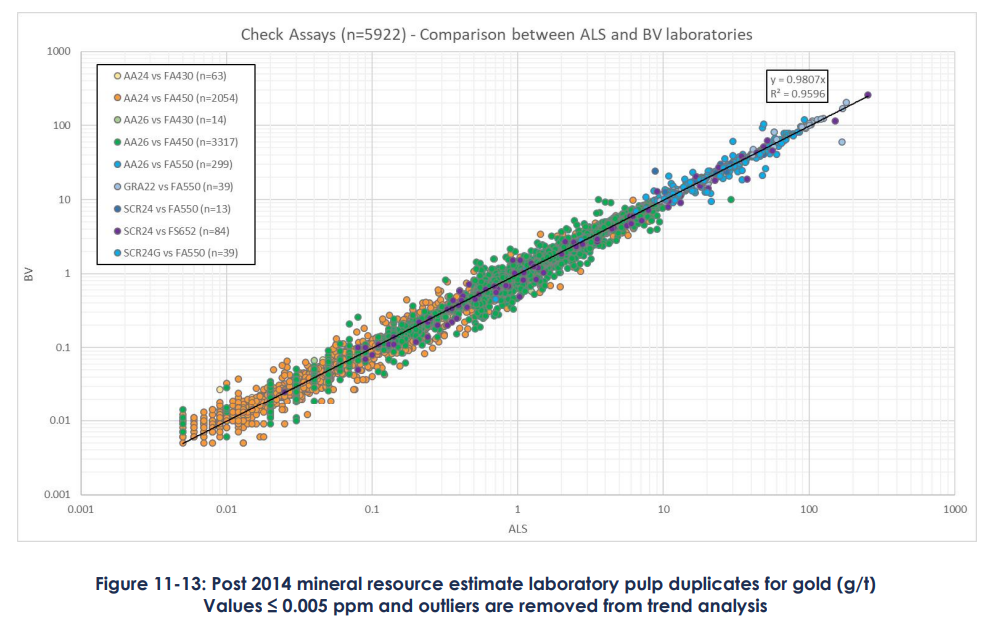
La Fig. 2 présente les résultats d’analyse des duplicatas. Une manière courante de présenter les duplicatas est sous la forme d’un nuage de points où l’abscisse correspond à la première valeur et l’ordonnée à la seconde valeur échantillonnée. Ici, l’échantillon 1 provient du laboratoire ALS, tandis que l’échantillon 2 provient du laboratoire BV. Une régression linéaire est réalisée sur ce nuage de points afin d’identifier la droite de corrélation et le coefficient de détermination .
Aucun élément anormal n’a été observé. On ne note pas de biais apparent et la corrélation entre les deux séries d’analyses est forte (). Quelques écarts importants apparaissent, mais ils sont attendus dans ce type d’analyse en échelle log-log.
Échantillons de référence à teneur connue¶
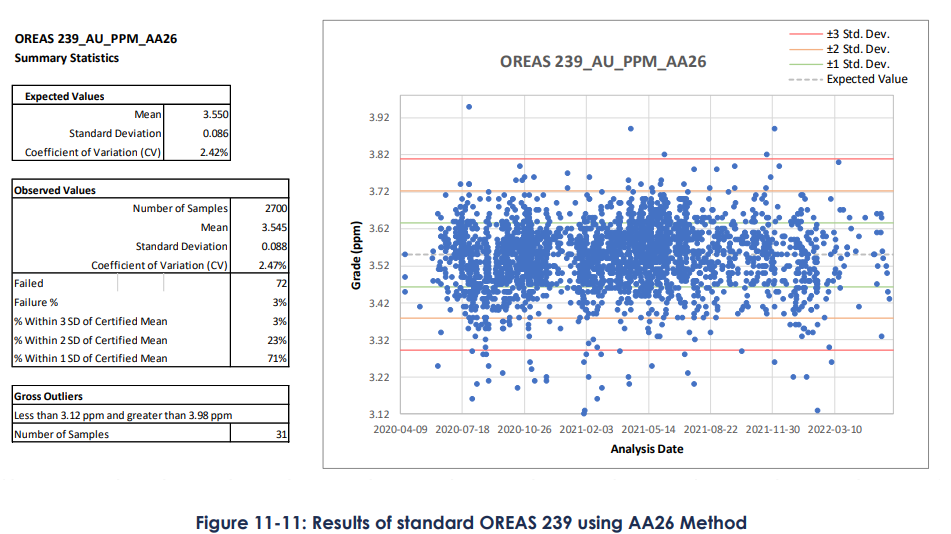
La Fig. 3 présente les résultats d’analyse des standards. Comme pour les blancs, les résultats sont présentés sous la forme d’une série temporelle. Connaissant à l’avance l’erreur sur nos standards (données fournies par le fabricant des standards), il est possible de construire des intervalles de confiance autour de la moyenne des standards (1, 2, 3 écarts-types). On s’attend à ce que 5 % des données se situent entre et 1 % entre , environ.
Ici, les analyses sont jugées très satisfaisantes. Les résultats suivent bien les valeurs de référence. La moyenne de la population des standards est de 3,55, tandis que le laboratoire a retourné une moyenne de 3,545. L’écart-type attendu est de 0,086, et celui obtenu par le laboratoire est de 0,088. Le coefficient de variation est de 2,42 % pour les standards et de 2,47 % pour les résultats retournés. Il n’y a rien à signaler.
Exemple 2) Mine Dumont, Royal Nickel¶
Voici un résumé des information pouvant être tiré du rapport technique NI-43-101 de la propriété Royal Nickel- Mine Dumont daté de 2013.
Les accès à la carothèque sont protégés par un système d’alarme zoné.
Les laboratoires sont certifiés ISO 9001:2000.
Les sacs d’échantillons sont scellés dès la récolte de l’échantillon.
Un blanc est inséré tous les 25 échantillons. Le blanc est constitué de sable contenant environ 0--80 ppm de Ni. Le sable est facilement identifiable en laboratoire.
La procédure de préparation d’échantillons au laboratoire est la suivante :
concassage de la roche reçue à 2 mm (70% passant),
sélection de 100 g,
pulvérisation à 106 m,
analyse.
Des duplicatas (1 sur 25) sont envoyés. Il s’agit de quarts de carottes, ce qui les rend relativement faciles à identifier comme duplicatas.
Quatre échantillons de matériel de référence certifié (EMRC ou « standard ») différents ont été utilisés.
Blancs¶
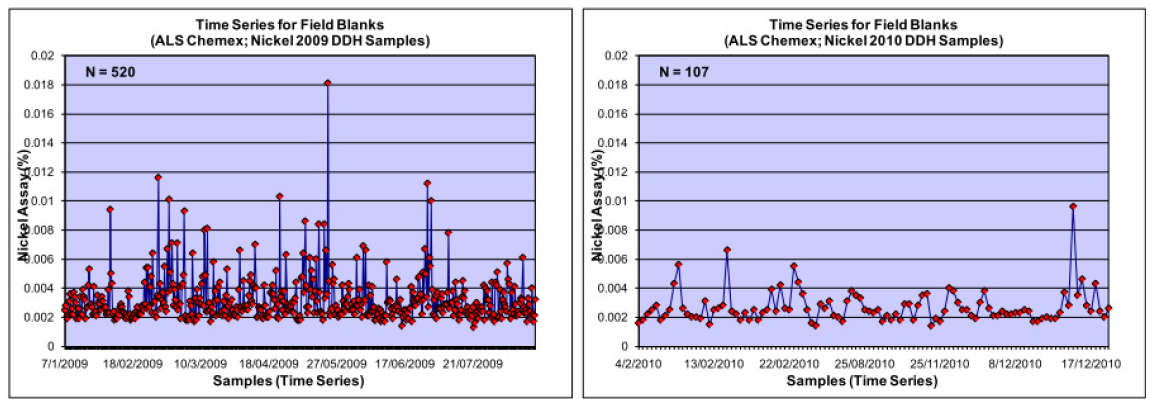
La Fig. 4 présente les résultats d’analyse des blancs. On constate que les teneurs analysées sont majoritairement toutes inférieures à 0,02 %. Il n’y a rien d’anormal à signaler : aucune contamination n’est observée. À noter que les blancs sont des échantillons de sable. Il est fort probable qu’un sable soit facilement repéré au laboratoire, indiquant qu’il s’agit bien d’un blanc. Il faut donc rester vigilant face aux éventuels comportements malveillants de certains laboratoires.
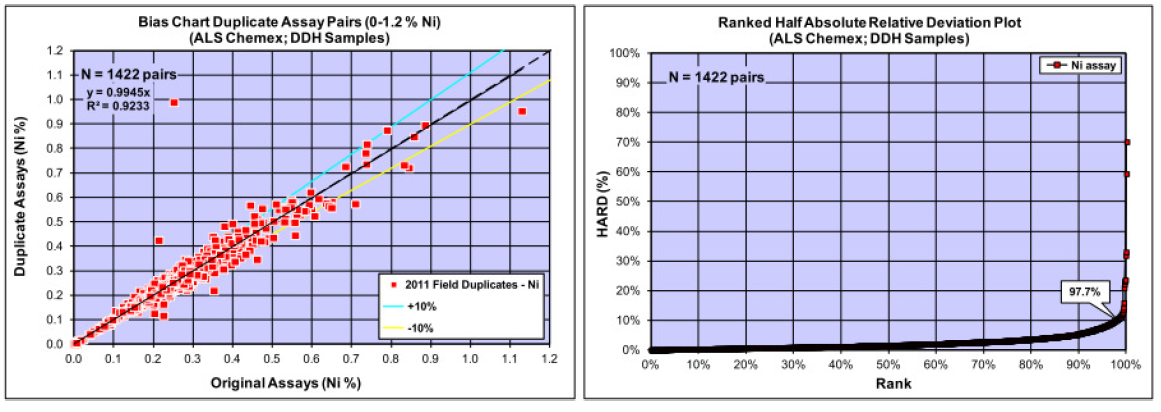
Duplicatas¶
La Fig. 5 présente les résultats d’analyse des duplicatas. Une seconde méthode d’analyse est également présentée : le graphique HARD (Half Absolute Relative Difference - demi-différence relative absolue). L’atelier interactif propose sa construction et son interprétation. À savoir, la courbe noire doit rester sous la coordonnée (0.9 ; 0.1), ce qui est bien le cas ici.
Ainsi, rien d’anormal à signaler, excepté que 2,3 % des points sur la figure de gauche devraient dépasser la limite de ±10 % relative pour le demi-écart. Difficilement observable. La figure de droite confirme cette proportion exacte de 2,3 % (soit 100 % - 97,7 %).
Le problème provient du tracé des lignes ±10 % sur la figure de gauche, qui ne correspondent pas exactement à la limite indiquée à droite. Il s’agit donc d’un problème d’affichage des résultats, sans impact sur la précision des analyses.
Échantillons de référence à teneur connue¶
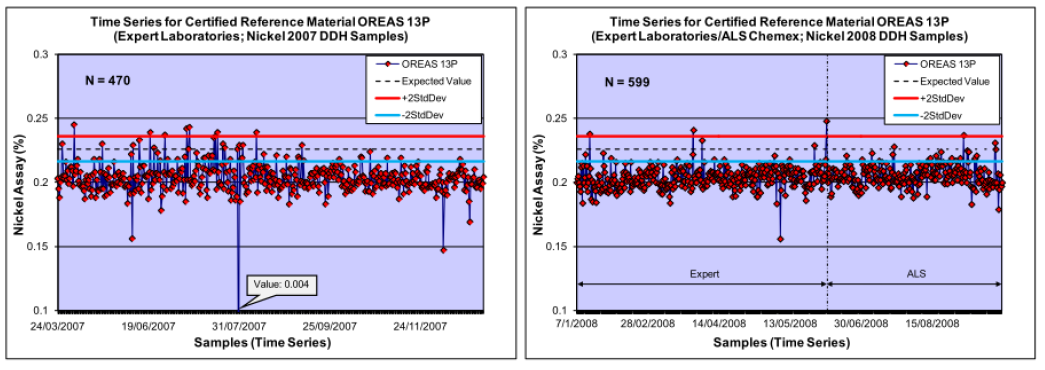
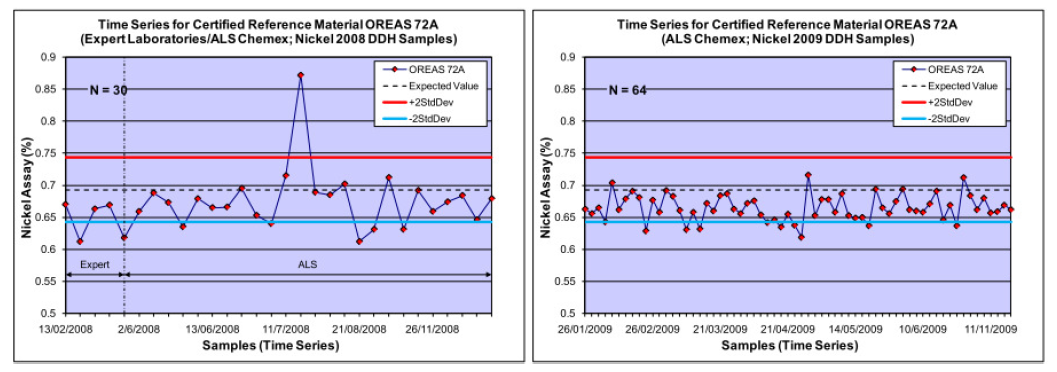
La Fig. 6 et la Fig. 7 présentent les analyses réalisées par deux laboratoires différents sur deux périodes distinctes, portant sur quatre échantillons de matériel de référence certifié (EMRC ou « standard »).
On constate que la majorité des analyses (points rouges) sont systématiquement inférieures à la moyenne des standards (ligne pointillée noire), quel que soit le standard utilisé ou le laboratoire.
Cela indique un problème de biais important pour les deux laboratoires, qui sous-estiment les teneurs réelles en nickel des standards.
Outils statistique pour le contrôle qualité¶
Selon Abzalov (2011)[3], la statistique la plus utile en contrôle de qualité des duplicatas est le coefficient de variation (CV), défini par :
où est l’écart-type expérimental de la paire de duplicatas, et la moyenne des duplicatas.
Dans le cas d’une paire de duplicatas, notée et , on a :
Ce qui donne :
D’autres auteurs utilisent des statistiques équivalentes telles que :
Le HARD (Half Absolute Relative Deviation), défini comme :
Le AMPD (Absolute Mean Percentage Difference), défini comme :
On observe que toutes ces statistiques sont directement proportionnelles entre elles, alors aussi bien utiliser le CV directement.
Rôle de l’ingénieur géologique et minier¶
Chaque type de minéralisation et chaque environnement minier constitue un cas particulier où la précision de l’échantillonnage dépend du sens pratique et de l’esprit critique du géologue, de l’ingénieur géologique ou de l’ingénieur minier. Celui-ci doit s’assurer que les échantillons sont les plus représentatifs possibles. Il doit également tenir compte des contraintes budgétaires et de production, puisque l’échantillonnage ne doit pas ralentir l’exploitation.
Remarque 1¶
L’échantillon le plus proche de l’échantillon parfait est la carotte obtenue par forage au diamant. L’ingénieur géologue utilise ces échantillons lors des phases d’exploration, de définition et de mise en valeur pour prédire les ressources et réserves du gisement. Les estimations ainsi produites peuvent, dans certains cas, être comparées aux teneurs réellement obtenues lors de la production.
Remarque 2¶
Puisque chaque échantillon est extrapolé pour représenter un ensemble plus vaste, il doit conserver une certaine homogénéité. Si un échantillon s’écarte trop de l’ensemble des teneurs, cela peut indiquer un événement fortuit, comme la présence d’une pépite d’or significative.
Dans l’industrie minière, il est courant de modifier ces teneurs anormalement élevées. Les pratiques habituelles incluent notamment :
L’exclusion pure et simple de ces échantillons ;
Leur réévaluation à la valeur des échantillons voisins ;
Leur plafonnement systématique à une valeur limite (par exemple, 1 oz Au/t) ;
L’application d’une correction basée sur la distribution statistique des teneurs ;
Le rééchantillonnage ou la reprise de l’analyse.
D’un point de vue statistique, chacune de ces approches est incorrecte et introduit un biais systématique conduisant à une sous-estimation des teneurs (biais conservateur). Cependant, comme les teneurs obtenues lors de la production sont souvent inférieures aux teneurs estimées (biais conditionnel — voir les lectures sur la géostatistique), ces pratiques peuvent rapprocher les estimations des valeurs de production.
Cette situation illustre un cas où une seconde erreur compense partiellement la première, ce qui explique sans doute en partie la popularité de ces méthodes.
Partie de la roche envoyée pour analyse qui n’est pas utilisée par le laboratoire. Elle est habituellement retournée à la mine.
Partie de la roche qui est pulvérisée pour l’analyse chimique.
Abzalov, M. (2011). Sampling Errors and Control of Assay Data Quality in Exploration and Mining Geology. In Applications and Experiences of Quality Control. InTech. Abzalov (2011)
- Abzalov, M. (2011). Sampling Errors and Control of Assay Data Quality in Exploration and Mining Geology. In Applications and Experiences of Quality Control. InTech. 10.5772/14965