Abstract¶
Ce chapitre présente les fondements et les applications des simulations géostatistiques, un domaine clé pour la modélisation des variables spatiales complexes. Les simulations permettent de représenter l’incertitude spatiale et de générer des réalisations possibles cohérentes avec les données observées. Nous abordons les différences entre estimation et simulation, les types de simulations non conditionnelles et conditionnelles, ainsi que les méthodes classiques telles que la décomposition de Cholesky et la simulation séquentielle gaussienne (SGS). Ce chapitre fournit aussi les critères pour choisir et appliquer ces méthodes, analyse leurs avantages et limites, et illustre l’interprétation des résultats dans le contexte de l’évaluation des ressources.
Introduction aux simulations géostatistiques¶
Au cours des vingt dernières années, les simulations géostatistiques ont pris une place centrale dans la pratique moderne de la géostatistique. Leur importance s’explique par le fait que de nombreux problèmes d’ingénierie, d’environnement et de ressources naturelles impliquent des relations non linéaires entre les variables ou des transformations non linéaires des données. Dans de tels contextes, une estimation ponctuelle ou même un modèle spatial moyen n’est pas suffisant : il devient essentiel de reproduire la variabilité spatiale complète du phénomène étudié, ce que permettent précisément les simulations géostatistiques.
Les simulations deviennent particulièrement indispensables lorsque les propriétés recherchées changent avec l’échelle d’observation. C’est le cas, par exemple, de la transmissivité ou de la conductivité hydraulique, dont l’estimation dépend à la fois de la taille du bloc considéré, du type de test réalisé ou des conditions aux limites utilisées dans un modèle d’écoulement. De même, lorsque deux variables entretiennent une relation non linéaire — comme la charge hydraulique et la transmissivité, ou encore le champ gravimétrique et la densité — la préservation de la structure spatiale devient fondamentale pour produire des prédictions fiables. Les simulations sont également essentielles lorsque les processus physiques sont décrits par des fonctions de transfert complexes, comme c’est le cas en conception de piles d’homogénéisation, en simulation de la variabilité des teneurs en usine, ou en modélisation du temps de transport d’un contaminant.
Un point clé à retenir est que la connaissance de la moyenne locale n’est pas toujours suffisante pour représenter correctement un phénomène. Dans certains cas, comme l’évaluation du profit d’un bloc minier, seule la teneur moyenne est nécessaire : le rendement dépend essentiellement de cette moyenne et des coûts d’exploitation. En revanche, d’autres phénomènes sont extrêmement sensibles à la structure spatiale interne du bloc. C’est le cas, par exemple, de la conductivité hydraulique dans un milieu hétérogène composé de sable et d’argile : la conductivité effective dépend certes de la proportion relative de ces matériaux, mais surtout de la manière dont ils sont spatialement organisés. Deux blocs ayant les mêmes proportions peuvent présenter des conductivités radicalement différentes si les matériaux sont disposés de manière plus ou moins connectée, orientée ou anisotrope.
La Fig. 1 illustre ce principe. On y observe deux blocs présentant une même proportion de sable et d’argile, mais des architectures internes très différentes. Si l’on prenait naïvement la moyenne arithmétique des transmissivités (par exemple pour le sable et pour l’argile), on obtiendrait une transmissivité moyenne équivalente à . Cependant, cette valeur est incorrecte, car la transmissivité effective d’un bloc dépend du mode de connexion des matériaux : - lorsque les matériaux alternent verticalement, la transmissivité effective s’obtient par la moyenne harmonique, typique d’un écoulement en série ; - lorsque les matériaux alternent horizontalement, la transmissivité effective correspond plutôt à la moyenne arithmétique, typique d’un écoulement en parallèle ; - lorsqu’ils sont mélangés finement, c’est la moyenne géométrique qui s’impose. Ces trois situations conduisent à des résultats extrêmement différents, malgré un histogramme identique : 50% de faciès bleus et 50% de faciès rouges.
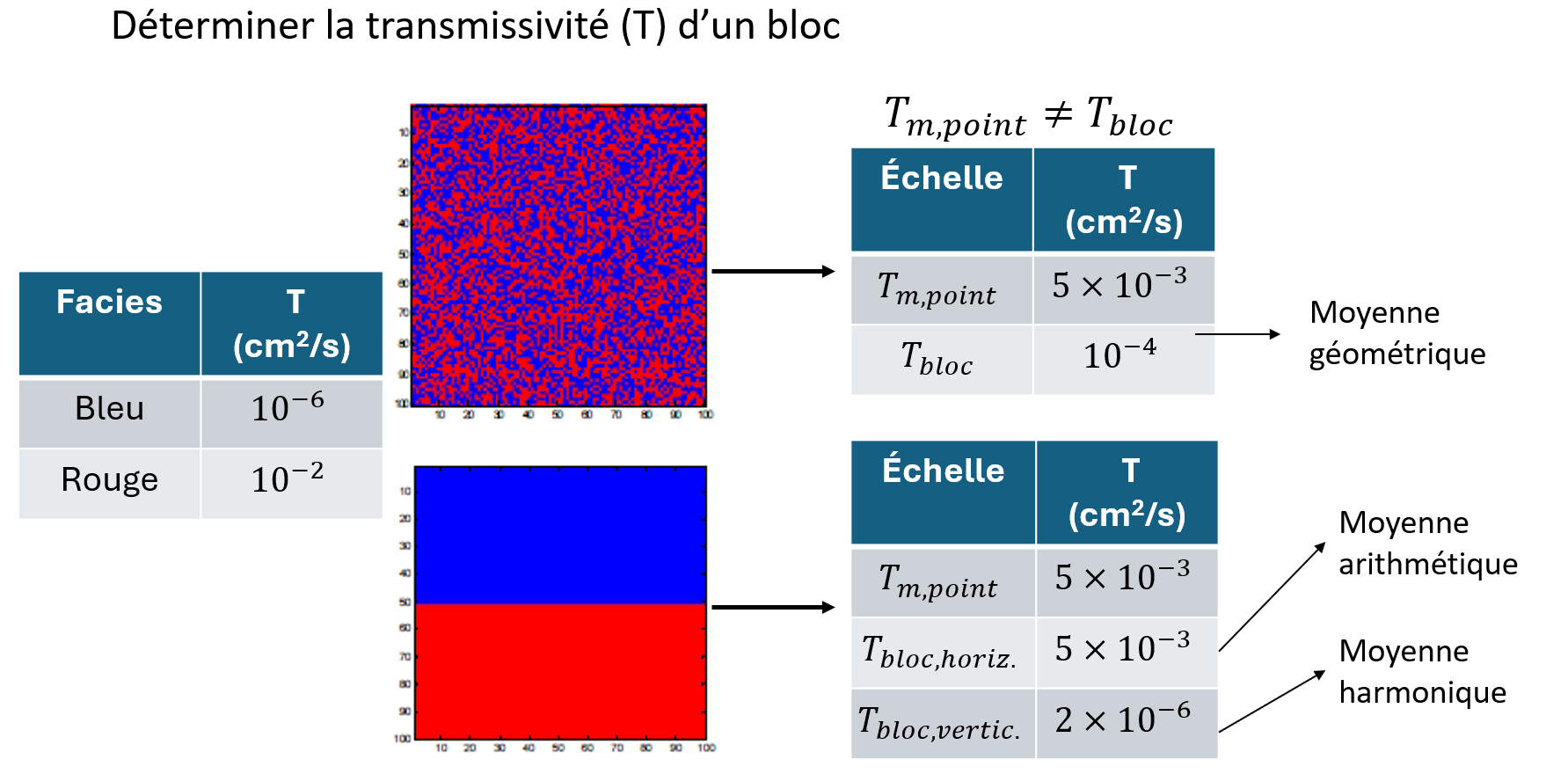
Figure 1:Impact de la structure spatiale sur la transmissivité effective.
Cet exemple met en évidence un point fondamental : deux blocs peuvent présenter exactement les mêmes proportions de matériaux, et donc le même histogramme global, tout en ayant des propriétés effectives radicalement différentes en raison de leur agencement interne. Ce n’est pas la proportion seule qui importe, mais la manière dont les matériaux sont organisés et connectés dans l’espace. Selon que les phases sont disposées verticalement, horizontalement ou de manière mélangée, la transmissivité effective d’un bloc peut varier de plusieurs ordres de grandeur.
Ce constat illustre pourquoi les simulations géostatistiques sont essentielles : elles permettent de représenter explicitement les structures spatiales — continuités, connexions, orientations — qui contrôlent les propriétés hydrauliques ou physiques d’un milieu. Même lorsque deux domaines possèdent la même distribution globale de valeurs, leurs comportements peuvent être complètement différents si leurs structures internes ne sont pas les mêmes. C’est précisément cette dimension spatiale que les méthodes de simulation permettent de capturer.
En somme, les simulations géostatistiques constituent la seule approche capable de préserver simultanément les proportions globales, la variabilité locale et les connexions spatiales entre les matériaux. Elles offrent une représentation beaucoup plus fidèle de la réalité physique, en particulier pour les phénomènes régis par des relations non linéaires ou fortement influencés par la géométrie interne des blocs. Leur utilisation est donc indispensable dès que la structure spatiale joue un rôle déterminant dans le comportement du système.
Dans ce chapitre, nous nous concentrerons sur les simulations géostatistiques de processus continus et gaussiens. Le chapitre suivant abordera quant à lui la modélisation des faciès, qui fait intervenir des variables discrètes et des structures catégorielles plus complexes.