10.5 Krigeage mou (« soft kriging ») ou krigeage avec données incertaines

Le krigeage d’indicatrices permet d’étendre immédiatement l’information à des données imprécises ou incertaines.

Exemple :
Considérons le problème de cartographier la profondeur du toit d’un réservoir pétrolier. Les forages pétroliers étant coûteux, les données sont généralement peu nombreuses. De plus, certains forages doivent parfois être abandonnés après plusieurs centaines de mètres sans atteindre le toit du réservoir. La Fig. 2 illustre ce phénomène. On constate qu’une estimation obtenue par krigeage ordinaire peut violer l’information partielle disponible : le toit estimé se situe alors dans une zone où le forage indique clairement que la profondeur réelle doit être supérieur.

Le krigeage ordinaire intègre difficilement ce type d’information incomplète. En revanche, le krigeage d’indicatrices (KI) permet de le faire directement et naturellement.

On dispose ici de l’information suivante :

Z(x_i) > 500 \text{ m}

(1)

On définit alors la variable indicatrice :

I(x,c) = \begin{cases} 1 & \text{si } Z(x) \leq c, \\ 0 & \text{sinon}. \end{cases}

(2)

Pour tous les seuils $c$ inférieurs à 500 m, on peut coder

I(x_i, c) = 0,

(3)

puisque l’on sait que la profondeur dépasse cette valeur.

Pour les seuils supérieurs à 500 m, la donnée est absente et ne peut donc pas être codée. Ainsi, pour les profondeurs inférieures à 500 m, on dispose de quatre indicatrices, tandis qu’au-delà de 500 m, seules trois données restent utilisables, car l’information fournie par l’inégalité ne permet plus de préciser la valeur de l’indicatrice. Le krigeage d’indicatrices permet donc d’intégrer ces données d’inégalité de manière simple : il suffit d’en tenir compte lors du codage des indicatrices. La seule différence réside dans le fait que le nombre de données disponibles varie d’un seuil à l’autre, en fonction des relations d’inégalité accessibles.

La Fig. 1 présente, dans le cadran supérieur droit, le résultat du krigeage d’indicatrices. On constate clairement que l’espérance conditionnelle obtenue par cette méthode respecte l’information fournie par le forage n’ayant pas rencontré le toit : l’estimation ne franchit plus la profondeur minimale imposée par cette donnée d’inégalité.

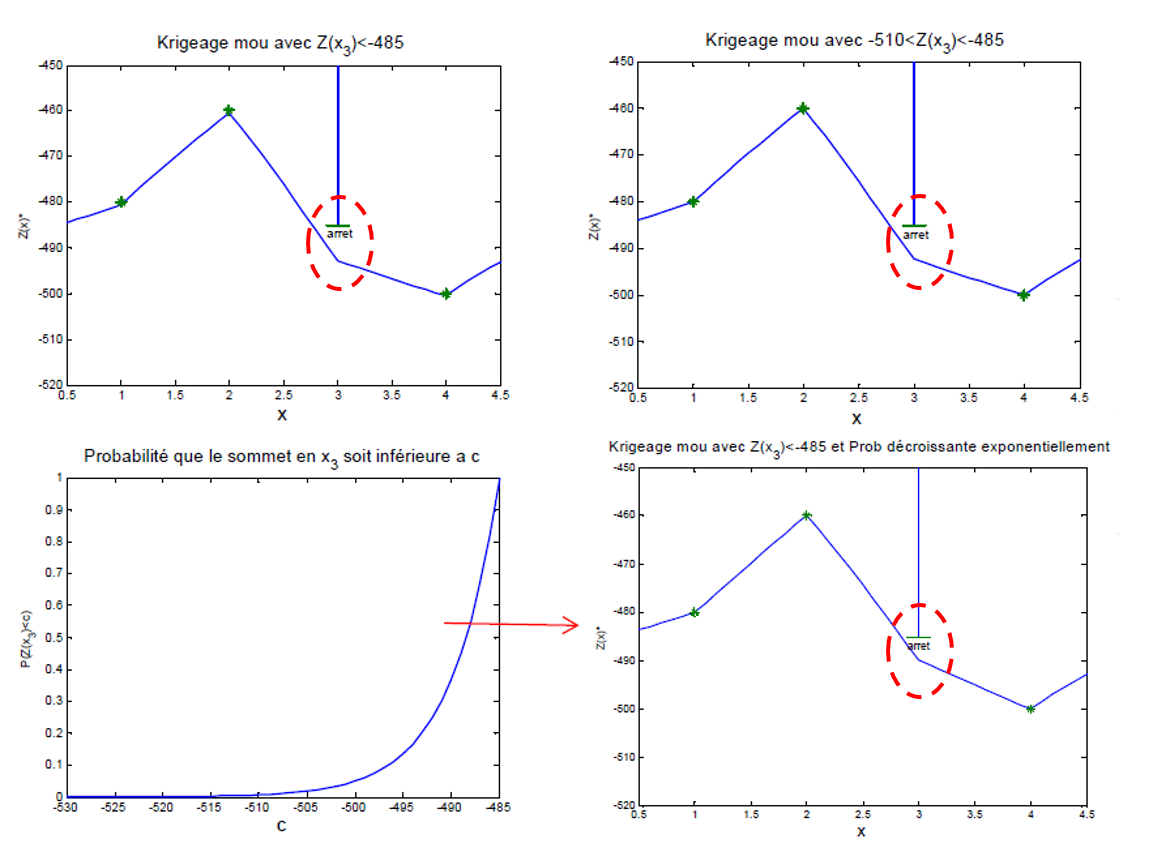
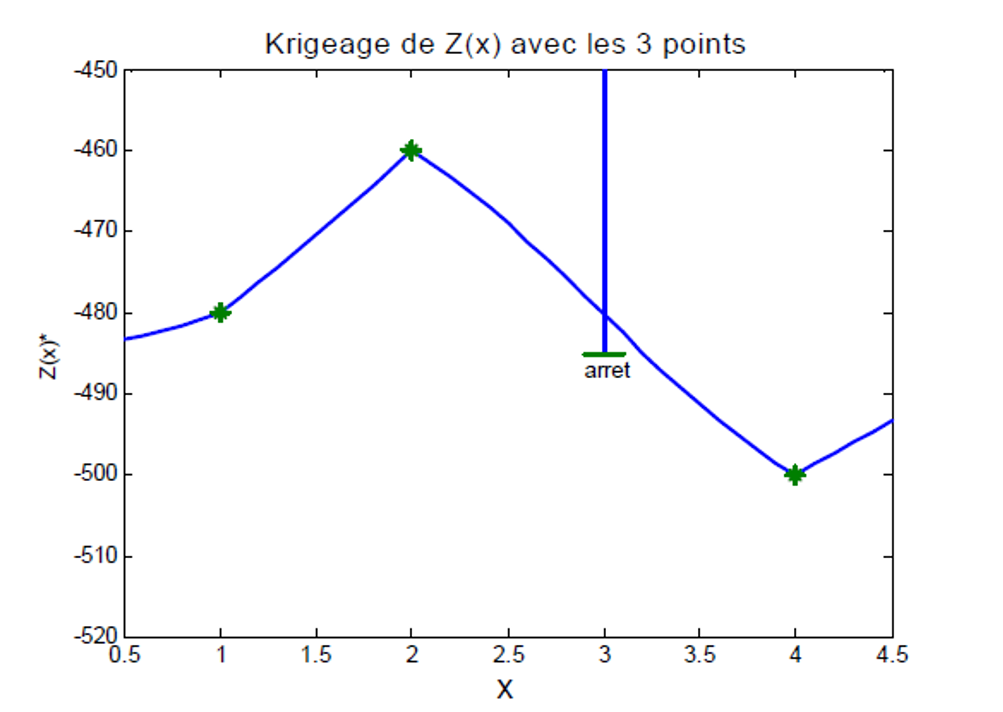
Figure 1:Exemple de violation d’une donnée incertaine par krigeage ordinaire.

Autre exemple dans le domaine pétrolier :
On peut également disposer de valeurs sismiques fournissant une estimation approximative, mais incertaine, de la profondeur du toit du réservoir. Ces profondeurs sismiques incertaines peuvent être représentées sous la forme de fonctions de répartition. Ces fonctions peuvent ensuite être utilisées directement pour coder les indicatrices en fonction des différents seuils, ce qui permet d’intégrer explicitement l’incertitude dans le krigeage. La Fig. 1 illustre ce principe dans les deux cadrans inférieurs : la figure de gauche présente la fonction de répartition déduite du levé géophysique, tandis que la figure de droite montre son impact sur l’espérance conditionnelle obtenue par krigeage d’indicatrices.

Ainsi, le krigeage d’indicatrices s’adapte naturellement à la prise en compte de données partielles, manquantes ou incertaines, ce qui constitue un avantage important dans les applications pratiques.