Abstract¶
Cette section présente la théorie permettant de déterminer la teneur de coupure optimale pour les opérations minières. La définition des paramètres y est exposée, ainsi que des ateliers interactifs permettant d’étudier l’impact des paramètres opérationnels et économiques sur la rentabilité des projets miniers.
Terminologie¶
Stérile
Roche qui est retirée au cours de l’exploitation minière pour pouvoir accéder aux matériaux minéralisés et qui n’est pas traitée davantage pendant l’année de déclaration.
Matériau minéralisé
Volume de roche susceptible de contenir du minerai.
Minerai
Portion économiquement rentable du matériau minéralisé.
Concentrateur (ou usine de traintement)
Une installation industrielle utilisée dans le processus de traitement des minerais pour séparer les minéraux de valeur des autres composants du minerai.
Teneur
Quantité d’un élément contenu dans un mélange, exprimée en pourcentage.
Teneur de coupure
La teneur minimale d’un élément contenu dans un mélange qui justifie son extraction et son traitement de manière économiquement viable.
Teneur de coupure optimale
Teneur de coupure permettant de maximiser le profit net par tonne de matériau minéralisé.
Teneur de coupure limite
Teneur de coupure permettant de maximiser le profit net par tonne de matériau minéralisé pour une composante spécifique des opérations minières.
Teneur de coupure d’équilibre
Teneur de coupure permettant de maximiser le profit net par tonne de matériau minéralisé pour une maximisation simultanée de deux composantes spécifiques des opérations minières[1].
Définitions des variables¶
La plupart des opérations minières comportent trois étapes principales : l’extraction, la concentration et la mise en marché — chacune ayant ses propres coûts associés ainsi qu’une capacité maximale, voir limite.
La théorie de Lane et Taylor repose sur plusieurs variables économiques, permettant d’estimer les revenus d’une minière ainsi que les coûts liés à son ouverture, son exploitation et sa fermeture.
Mise en contexte des variables¶
Supposons une tonne de matériau minéralisé illustrée à la Fig. 1. Les blocs de couleur jaune ont une teneur () supérieure ou égale à la teneur de coupure (i.e., ), tandis que les blocs bleus ont une teneur inférieure à (i.e., ). Ainsi, l’ensemble des blocs jaunes constitue notre minerai, la portion économiquement rentable du matériau minéralisé.
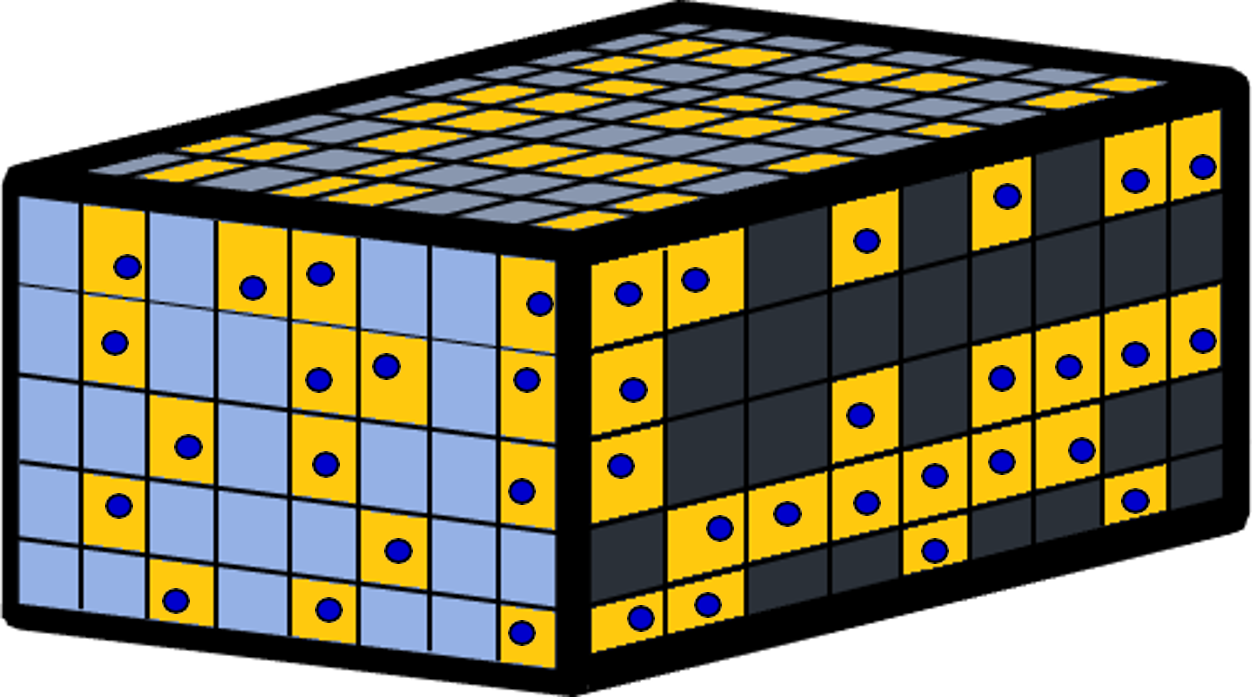
Figure 1:Évolution de la teneur de coupure selon la méthode utilisée.
Teneur de coupure¶
La teneur de coupure joue un rôle fondamental dans l’évaluation économique et la planification des projets miniers. Elle permet notamment de :
Distinguer le minerai du stérile
Elle sert de seuil décisionnel pour déterminer si un bloc de matériau minéralisé est suffisamment riche en minerai pour être traité ou s’il doit être rejeté.
Maximiser la valeur économique du gisement
En ajustant la teneur de coupure, on peut optimiser le profit net global, en tenant compte des contraintes économiques, techniques, sociétales, législatives et environnementales.
Planifier l’exploitation minière
Elle guide les choix relatifs à l’ordre d’extraction, à la durée de vie de la mine et à l’adaptation du plan minier selon les fluctuations de ces même contraites.
Évaluer les ressources et réserves
Elle permet de classifier les ressources minérales en ressources exploitables (réserves) ou non économiques, selon les critères définis par les standards internationaux (ex. : CIM, JORC).
Prendre des décisions stratégiques
Elle peut être ajustée dynamiquement selon les capacités de traitement, les contraintes de marché ou les politiques internes de l’entreprise.
Ainsi, la teneur de coupure n’est pas une valeur fixe, mais un paramètre stratégique dynamique qui influence directement la rentabilité, la durabilité et la gestion des opérations minières. La théorie entourant la teneur de coupure est complexe et vaste. En étudier tous les détails requiert un cours à part entière. Ici, nous nous concentrerons sur l’impact des opérations minières sur la teneur de coupure et comment nos décisions en tant qu’ingénieurs peuvent influencer ou modifier cette teneur. Nous aborderons que la théorie de Lane (ou théorie de Taylor) dans le cadre de ce cours.
Nous pourrions optimiser en fonction de plus de deux composantes, mais cela rend la démarche beaucoup plus complexe et n’ajoute pas nécessairement plus de précision en raison des hypothèses qui doivent être posées.