Abstract¶
Ce chapitre présente les principales méthodes de simulation de faciès utilisées en géostatistique. Il couvre les approches classiques, telles que la simulation d’indicatrices, la simulation gaussienne tronquée ainsi que la simulation plurigaussienne, de même que des méthodes plus avancées comme les simulations multipoints. Chaque technique est décrite en détail, en mettant en évidence ses fondements théoriques, ses avantages, ses limites et ses domaines d’application. Nous verrons également comment conditionner ces méthodes aux faciès observés en forages. L’objectif du chapitre est de fournir les bases théoriques et pratiques nécessaires à la mise en œuvre, à l’analyse et à l’interprétation des simulations de faciès dans divers contextes géoscientifiques. Le chapitre se conclut par plusieurs exemples d’applications issus de la littérature scientifique, illustrant la pertinence et la diversité des approches présentées.
Mise en contexte¶
Les simulations conditionnelles permettent de générer des réalisations équiprobables d’un modèle géologique tout en respectant à la fois une structure spatiale prescrite et les données observées. Chaque réalisation représente un état possible de la fonction aléatoire sous-jacente. Alors que le krigeage vise à minimiser la variance d’estimation et produit des modèles spatialement lissés, les simulations géostatistiques préservent la variabilité naturelle du milieu. Cette variabilité est essentielle dans de nombreuses applications, notamment lorsque les propriétés du milieu — par exemple la perméabilité — influencent fortement la réponse hydrogéologique de l’aquifère. C’est d’ailleurs ce que nous avons exploré au chapitre précédent - les simulations de variables continues.
Cependant, que faire lorsque la variable régionalisée représente des faciès géologiques, c’est-à-dire une variable catégorielle ? Par exemple, les faciès peuvent correspondre aux séquences stratigraphiques des Basses-Terres du Saint-Laurent ou encore distinguer les types de roches susceptibles de générer du drainage minier acide de celles qui sont chimiquement inertes. Au final, un faciès est une catégorie qui définit l’unité géologique étudiée, et cette nature discrète nécessite des méthodes de simulation adaptées.
Dans ce cadre, plusieurs approches de simulation de faciès ont été développées afin de tenir compte de la nature catégorielle ou discrète des unités géologiques. Parmi les approches les plus courantes figurent la simulation séquentielle d’indicatrice, la simulation gaussienne tronquée, la modélisation par objets ainsi que les méthodes de statistiques multipoints. Chacune d’elles repose sur des hypothèses, des structures mathématiques et des capacités de représentation différentes.
Mise en contexte¶
Une application importante de la modélisation de faciès concerne la représentation de la sous-surface pour des besoins en géotechnique et en hydrogéologie. Supposons que l’on dispose de plusieurs forages géotechniques indiquant les unités stratigraphiques (p. ex. les dépôts du Quaternaire) ainsi que les lithologies associées à chacune de ces unités (p. ex. gravier, sable, silt, argile). Il devient alors possible de générer plusieurs modèles géologiques à partir de ces données de forage.
La Fig. 1 présente deux réalisations de la séquence stratigraphique composée de six unités, tandis que la Fig. 2 illustre deux réalisations de la lithologie.
À partir de ces réalisations, il est ensuite possible de caractériser l’aquifère régional (étude hydrogéologique) ou d’évaluer les risques géotechniques, notamment liés à la présence des argiles de la mer de Champlain. Les applications sont nombreuses et couvrent plusieurs domaines. Ici, les figures ont été tiré de l’article de Schorpp et al. (2022) en libre-d’accès du groupe de recherche en hydrogéologie stochastique de l’université de Neuchâtel en Suisse.
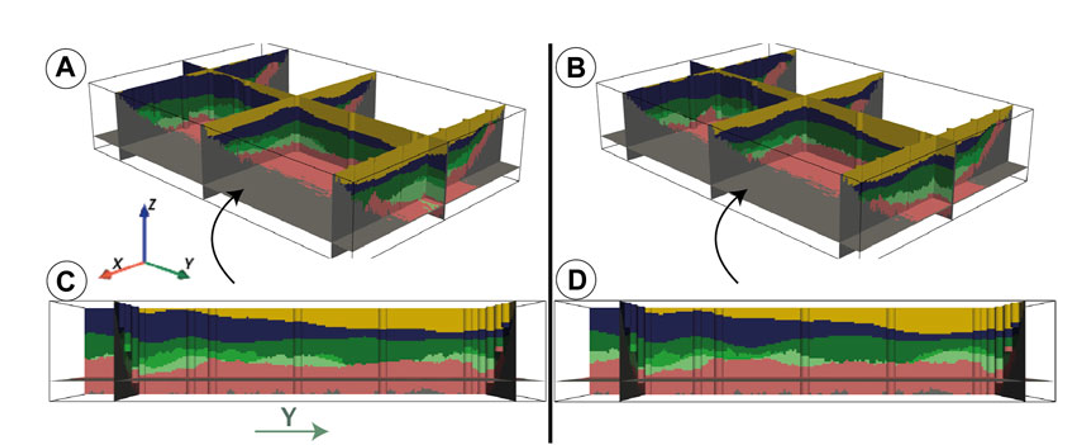
Figure 1:Deux réalisations conditionnelles de la stratigraphie, avec leur vue en coupe (A et B) et une vue de profil (C et D), simulées à l’aide de champs gaussiens.
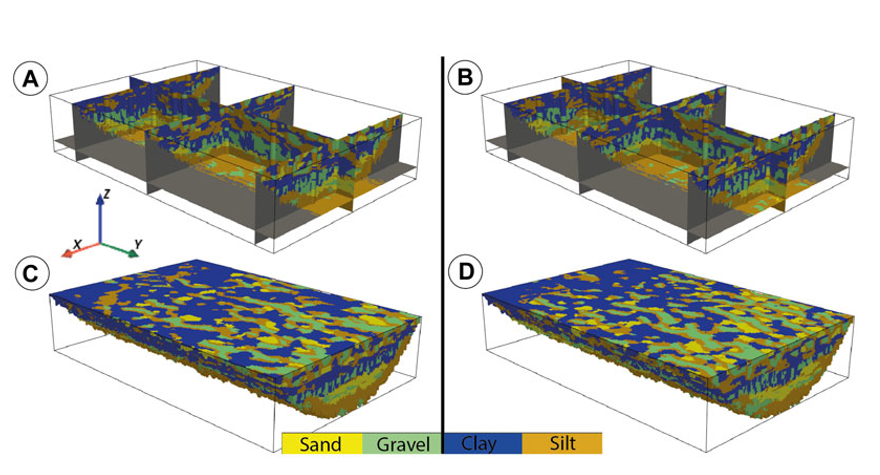
Figure 2:Deux réalisations conditionnelles de la lithologie, avec leur vue en coupe (A et B) et leur vue globale (C et D), simulées par une méthode multipoints.
Méthodes de simulation de faciès¶
Il existe quatre grandes approches pour la modélisation des faciès : la simulation séquentielle d’indicatrice, la simulation gaussienne tronquée , la modélisation par objets, et les statistiques multipoints.
Simulation séquentielle d’indicatrices (Sequential Indicator Simulation, SIS)
La SIS est une technique de simulation catégorielle basée sur le variogramme d’indicatrices. Elle est aujourd’hui intégrée dans la plupart des logiciels commerciaux de modélisation géostatistique. Le SIS ne requiert qu’un code de krigeage pour être implémenté, ce qui contribue largement à sa popularité. La SIS est particulièrement adaptée lorsque la géométrie des corps géologiques n’est pas clairement définie et que la continuité spatiale des faciès peut être décrite de manière satisfaisante à l’aide des variogrammes d’indicatrices. C’est typiquement le cas dans des environnements fortement diagenétisés ou altérés, où les structures sont diffuses et difficiles à représenter de manière déterministe. Au fil des années, plusieurs auteurs ont proposé des variantes intégrant différents estimateurs et l’utilisation de variables secondaires.
Simulation gaussienne tronquée (Truncated Gaussian Simulation, TGS)
La TGS est également une méthode fondée sur le variogramme, mais elle se passe sur un champ latent qui est tronqué pour le transformer en des facièes. Comparativement au SIS, la TGS permet un meilleur contrôle des transitions entre faciès, l’intégration de proportions non constantes via des courbes de proportions verticales, l’ajout de contraintes horizontales, ainsi qu’une représentation plus lisse des géométries en raison du modèle gaussien sous-jacent. La TGS est particulièrement appropriée dans des environnements présentant une variabilité modérée et des transitions de faciès bien définies.
Modélisation par objets
La modélisation par objets consiste à simuler des entités géométriques définies par un modèle mathématique décrivant leur forme, leur orientation, leur taille et leur fréquence. Elle est particulièrement efficace pour représenter des géométries complexes telles que les chenaux fluviatiles, leur sinuosité et leur continuité. Ses principales limites résident toutefois dans le nombre restreint de géométries disponibles et dans les difficultés de conditionnement aux données réelles.
Statistiques multipoints (MPS)
Les méthodes MPS décrivent la continuité spatiale à partir de configurations obtenues d’une image d’entraînement qui représente l’étendu de la complexité de la géologie. Elles permettent ainsi de reproduire des structures géologiques complexes, souvent impossibles à modéliser avec les variogrammes classiques. Le principal défi réside dans la conception d’une image d’entraînement à la fois réaliste, représentative et compatible avec les exigences de stationnarité. Malgré ces contraintes, les méthodes MPS offrent un potentiel considérable pour plusieurs architectures géologiques — il s’agit probablement des approches les plus puissantes lorsqu’une information géométrique riche est disponible.
- Schorpp, L., Straubhaar, J., & Renard, P. (2022). Automated Hierarchical 3D Modeling of Quaternary Aquifers: The ArchPy Approach. Frontiers in Earth Science, 10. 10.3389/feart.2022.884075