La simulation séquentielle d’indicatrices permet de modéliser la présence ou l’absence de faciès à partir de variables binaires (0 ou 1). Le processus repose sur une approche séquentielle similaire à celle de la simulation séquentielle gaussienne (SGS) utilisée pour les variables continues gaussiennes, mais adaptée ici au cas des variables catégorielles.
Algorithme¶
La méthodologie est très similaire à celle de la simulation séquentielle gaussienne ; il s’agit de son analogue dans le domaine catégoriel. Nous visitons les points de la grille selon un chemin aléatoire afin de simuler, à chaque emplacement, un faciès parmi les faciès possibles. La différence fondamentale réside dans la distribution utilisée : au lieu de tirer une valeur selon une distribution gaussienne conditionnelle obtenue par krigeage simple, nous tirons un faciès à partir d’une distribution catégorielle obtenue par krigeage d’indicatrices.
Concrètement, pour chaque faciès, on effectue un krigeage d’indicatrice afin d’estimer la probabilité que ce faciès soit présent au point considéré. Une fois les probabilités calculées (une par faciès), on forme un vecteur de probabilités qui doit sommer à 1. On tire ensuite au hasard un faciès selon cette distribution conditionnelle, ce qui permet d’obtenir le faciès au premier point visité. Comme pour la SGS, le faciès simulé est ajouté aux données conditionnantes (simulées et observées), puis l’on passe au point suivant, toujours choisi aléatoirement.
L’algorithme peut alors être expliqué comme suit :
Soit un champ de faciès et soit , , faciès observés :
On cherche à simuler en emplacements , , conditionnellement à .
Les étapes sont :
a) Coder chaque faciès par une indicatrice différente ;
b) Choisir un point aléatoirement et kriger les faciès en ce point conditionnellement aux données déjà simulées et observées pour obtenir les probabilités d’observer les faciès au point simulé soit les ;
c) Normaliser les probabilités (t.q. et ) ;
d) Tirer une valeur aléatoire de la loi , ce qui détermine le faciès simulé au point ;
e) Introduire le point aux données simulées et refaire le processus pour tous les points restants
(retour à l’étape b).
Remarques¶
Spatialement, toutes les transitions entre faciès sont possibles, car la méthode n’intègre aucune règle géologique explicite concernant l’ordre ou la compatibilité des contacts. Ainsi, des faciès qui ne devraient normalement jamais se toucher peuvent apparaître en contact direct dans les réalisations simulées si les données ne l’interdisent pas explicitement.
La méthode reproduit correctement les variogrammes d’indicatrices, garantissant une continuité spatiale conforme pour chaque faciès pris individuellement. Toutefois, elle ne reproduit pas les covariances croisées entre indicatrices, puisqu’elles ne sont pas utilisées dans le processus. En conséquence, les relations spatiales entre faciès — par exemple la tendance d’un faciès à en envelopper un autre, ou la présence de séquences privilégiées — ne sont pas modélisées, ce qui limite la représentation de structures géologiques complexes.
Tout comme dans la méthode SGS, l’utilisation d’un voisinage restreint peut nuire à la reproduction des structures spatiales définies par le variogramme de chaque indicatrice. Un voisinage trop petit, mal orienté ou hybride peut conduire à des réalisations biaisées qui ne respectent pas pleinement la continuité spatiale théorique du modèle.
Comme la méthode repose sur la simulation d’indicatrices, il est impossible d’obtenir des faciès présentant des frontières lisses. En conséquence, certains modèles de covariances — notamment le modèle gaussien — ne peuvent pas être reproduits par le SIS.
La méthode reste largement utilisé pour modéliser des faciès aux formes imprécises ou indéfinies, ou lorsque peu de données d’entrée sont disponibles.
Exemples¶
La Fig. 1 présente une réalisation avec les probabilités , et , en utilisant un variogramme sphérique de portée . Les faciès sont représentés par les couleurs suivantes : bleu pour , vert pour et brun pour . Notez que toutes les transitions possibles sont observées dans les deux sens et dans toutes les directions.
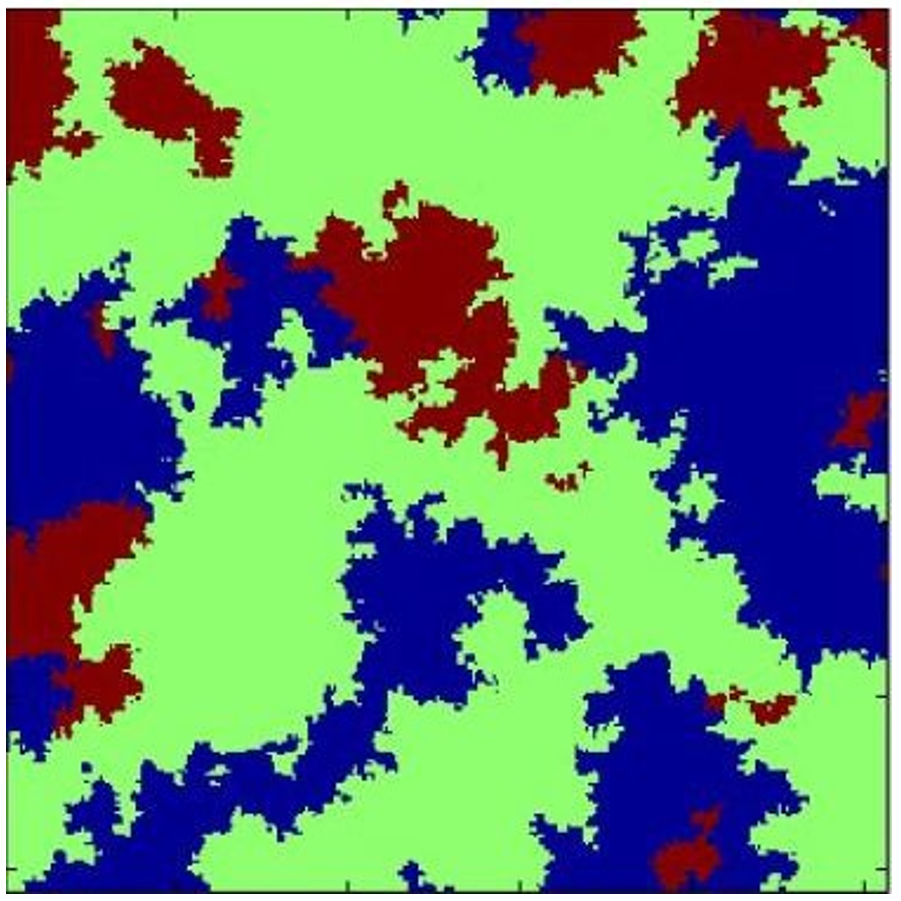
Figure 1:Simulation 2D isotrope.
La Fig. 2 présente une réalisation avec les probabilités , et , en utilisant un variogramme sphérique anisotrope de portée et . Les faciès sont représentés par les couleurs suivantes : bleu pour , vert pour et brun pour . On se rapproche plus d’une cas réaliste d’unité sédimentaire, mais néanmoins toutes les transitions sont possibles

Figure 2:Simulation 2D anisotrope.
La Fig. 3 présente une réalisation d’un modèle 3D plus réaliste obtenu par simulation séquentielle d’indicatrices. On observe que toutes les transitions entre faciès sont possibles. Il est important de rappeler que cette méthode est très utile dans des contextes où peu de données sont disponibles (les forages, représentés par les lignes noires) et lorsque les faciès présentent des formes imprécises ou difficilement définissables. Autrement dit, elle convient particulièrement aux situations où l’on dispose de peu d’information sur la connectivité et l’organisation spatiale des unités géologiques.
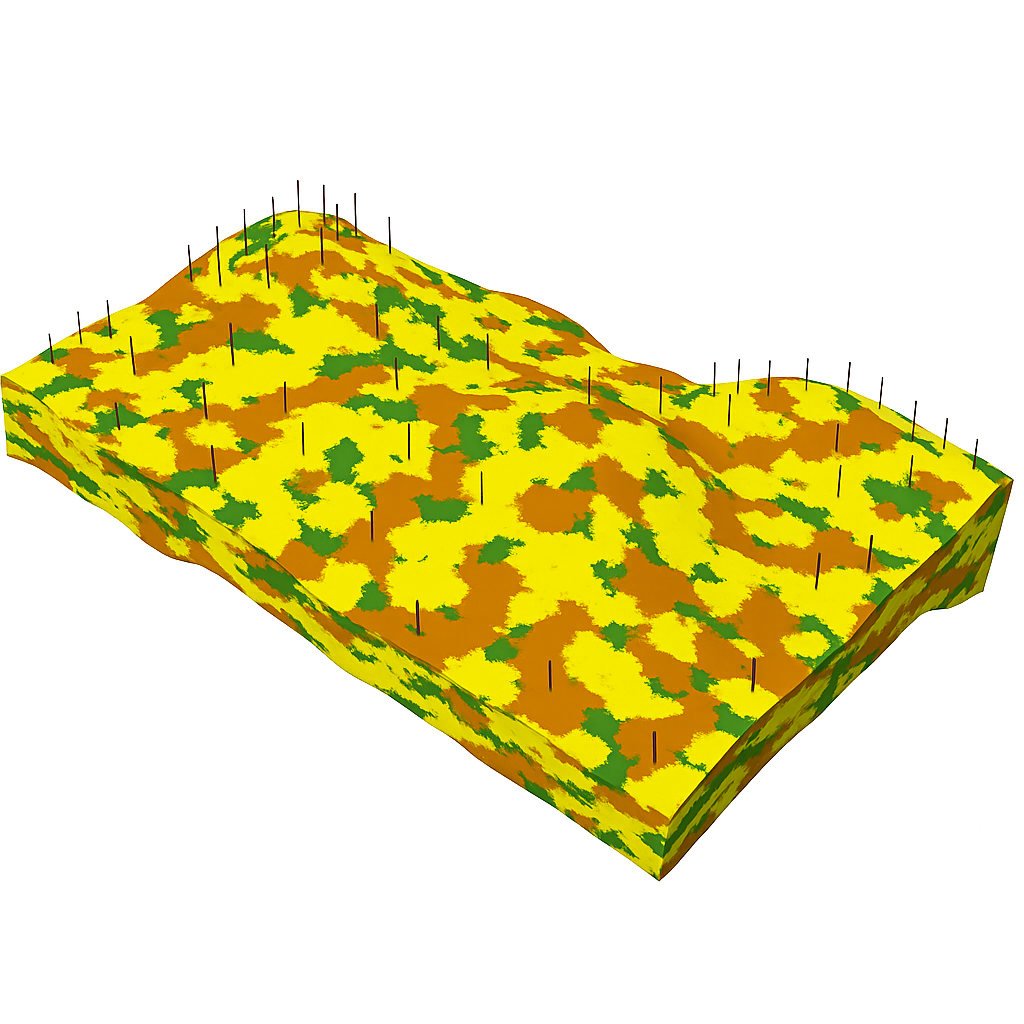
Figure 3:Une réalisation 3D plus réaliste d’un cas d’application réel.