Les simulations tronquées permettent de générer des variables catégorielles (faciès, lithologies, types de roches) à partir de champs gaussiens continus. Le principe est simple : on simule d’abord un ou plusieurs champs gaussiens en utilisant des méthodes géostatistiques classiques (LU, SGS, FFT-MA, bandes tournantes), puis on transforme ces champs continus en catégories en appliquant des seuils ou des zones de codage.
Cette approche permet de contrôler les proportions de chaque catégorie, de reproduire la continuité spatiale via le variogramme du champ gaussien, et, selon le modèle, d’imposer certaines relations spatiales entre les faciès (transitions permises ou interdites, proportions variables, etc.).
On distingue deux variantes principales :
la simulation gaussienne tronquée, qui utilise un seul champ gaussien découpé en intervalles ordonnés ;
la simulation plurigaussienne, plus flexible, qui combine plusieurs champs gaussiens pour définir des organisations spatiales plus complexes.
Simulation Gaussienne Tronquée¶
Le modèle gaussien tronqué simule une variable gaussienne continue, puis applique des seuils pour obtenir des faciès catégoriels respectant les proportions observées. L’algorithme non conditionnelle est assez simple :
Ordonnancement des faciès
Les faciès doivent être ordonnés (par exemple F1 < F2 < F3). Cet ordonnancement détermine les transitions possibles : seuls les faciès successifs peuvent être contigus dans l’espace, ce qui interdit par exemple une transition directe entre F1 et F3.Détermination des seuils gaussiens
À partir des proportions globales des faciès, on calcule les seuils gaussiens correspondants en utilisant les quantiles d’une loi normale standard . Ces seuils définissent les intervalles dans lesquels la valeur simulée du champ gaussien sera tronquée pour produire le faciès associé. La champ gaussian, que l’on considère comme latent, est de moyenne nulle et variance unitaire.Appliquer les seuils de codage. Une simulation gaussienne non conditionnelle est générée à l’aide d’une méthode classique (LU, SGS, FFT-MA, bandes tournantes). Une fois le champ continu obtenu, chaque valeur est comparée aux seuils déterminés à l’étape 2 : si elle tombe dans l’intervalle correspondant au faciès , la cellule est codée comme appartenant à ce faciès. Le champ gaussien est ainsi transformé en un champ catégoriel, garantissant les proportions souhaitées et les relations spatiales découlant du modèle.
La Fig. 1 présente un exemple d’application avec trois faciès, notés , et , dont les probabilités respectives sont , et . Les seuils de codage sont déterminés à partir de la fonction de répartition de la loi normale standard . Le premier seuil, , correspondant à la transition entre et , est donné par . Le second seuil, , correspondant à la transition entre et , est obtenu en cumulant les proportions des deux premiers faciès : . Toute valeur gaussienne inférieure à est alors codée , toute valeur comprise entre et est codée , et toute valeur supérieure à est codée . En utilisant un variogramme gaussien de portée 50 avec ces proportions, on obtient le champ de faciès illustré dans la Fig. 2, où l’on observe que la transition entre (bleu) et (rouge) doit obligatoirement passer par (vert); ainsi, et ne peuvent jamais être contigus.
Ainsi, le modèle implique que seuls les faciès successifs peuvent être contigus spatialement. Ainsi la transition − ne peut être observée. Le choix de l’ordre des faciès doit respecter les relations observées.
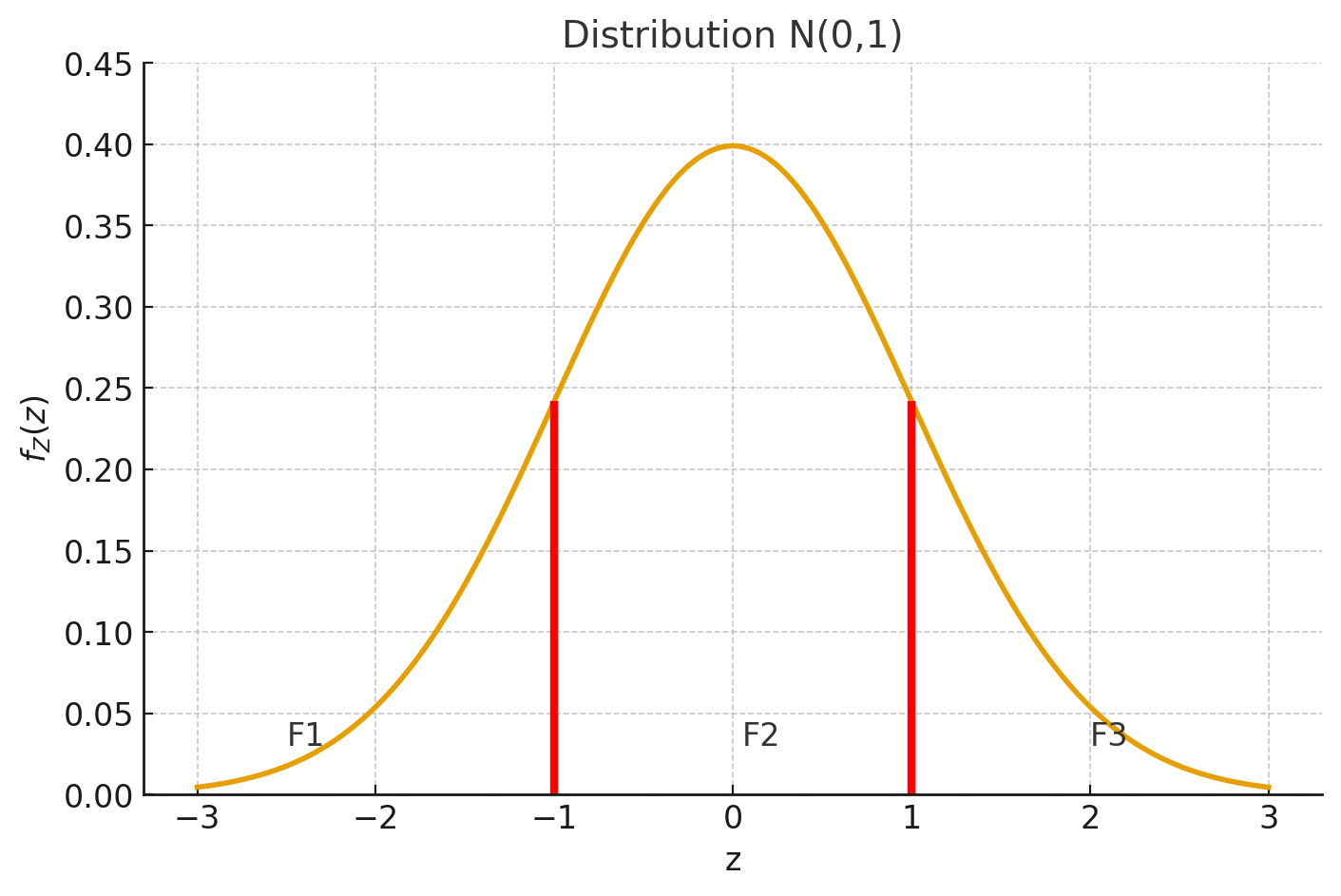
Figure 1:Exemple de seuil de codage pour une simulation gaussienne tronquée avec , et .

Figure 2:Exemple de simulation gaussienne tronquée réalisée à partir d’un champ latent gaussien suivant un variogramme gaussien de portée effective de 50 pixels, sur une grille de 250 par 250 pixels.
Comment décider du variogramme de la variable latente gaussienne?¶
Une difficulté importante de la méthode TGS réside dans l’identification de la structure spatiale du champ latent à modéliser. En effet, les données disponibles sont uniquement des faciès, c’est-à-dire des variables catégorielles. Nous ne disposons donc d’aucune variable continue permettant d’estimer directement un variogramme expérimental du champ gaussien latent. Les seules informations accessibles sont les variogrammes des indicatrices, qui ne se traduisent pas automatiquement en un variogramme latent unique. Il faut réaliser quelque manipulations mathématiques pour relier les variogrammes d’indicatrices aux variogramme de la structure latente continues.
Pour contourner ce problème, la méthode TGS s’appuie sur une calibration indirecte, basée sur les probabilités conjointes qui peuvent être estimées à partir des données de faciès. Ces probabilités correspondent à des intégrales de la loi binormale définies par la covariance latente inconnue. La stratégie consiste donc à ajuster la covariance (ou le variogramme) du champ gaussien latent de manière à ce que les probabilités binormales reproduisent au mieux les probabilités expérimentales.
Considérons une variable gaussienne latente et un champ catégoriel obtenu par troncature de . Notons
la probabilité d’observer simultanément le faciès en et le faciès en . Cette quantité peut être estimée empiriquement à partir des données. Il suffit de compter, pour chaque distance , le nombre de paires de points où l’on observe simultanément et , puis de normaliser par le nombre total de paires disponibles à cette distance. Ainsi, est simplement une fréquence relative observée.
La probabilité expérimentale peut s’estimer par :
où est le nombre total de paires de points séparées de la distance , et est la fonction indicatrice.
De plus, comme chaque faciès correspond à un intervalle de troncature du champ latent, on peut écrire :
Ainsi, la probabilité conjointe peut aussi s’écrire comme :
En revanche, la probabilité
peut être calculer théorique par l’intégrale de la densité binormale définie par la covariance du champ latent . Ainsi, pour chaque distance , les probabilités expérimentales imposent une contrainte sur la covariance gaussienne .
L’objectif est alors d’identifier la fonction de covariance qui minimise l’écart entre les probabilités théoriques issues du modèle binormal et leurs estimations empiriques obtenues à partir des données catégorielles.
La Fig. 3 présente le calcul théorique issu du modèle binormal. La surface colorée représente la densité de la loi normale bidimensionnelle associée au couple gaussien corrélé . Les lignes rouges indiquent les seuils de troncature et définissant respectivement les faciès et . Le calcul de la probabilité conjointe correspond alors à l’intégrale de cette densité binormale sur le rectangle délimité par ces seuils, c’est-à-dire à la quantité
où est la densité normale bidimensionnelle de moyenne nulle, de variance unitaire et de covariance .
La Fig. 4 présente les probabilités associées au modèle TGS considéré (rappel : , et ). On constate que les probabilités situées sur la diagonale sont décroissantes, ce qui s’explique par le fait que plus la distance augmente, plus la probabilité d’obtenir une paire de points appartenant à des faciès similaires devient rare. L’inverse se produit pour les transitions hors diagonale : il devient plus probable d’observer une transition entre deux faciès distincts lorsque la distance augmente. Il est également important de noter que pour , on observe bien pour , tandis que les probabilités entre faciès différents sont nulles. Enfin, lorsque , les probabilités convergent vers la limite .

Figure 3:Exemple de calcul théorique issu du modèle binormal.
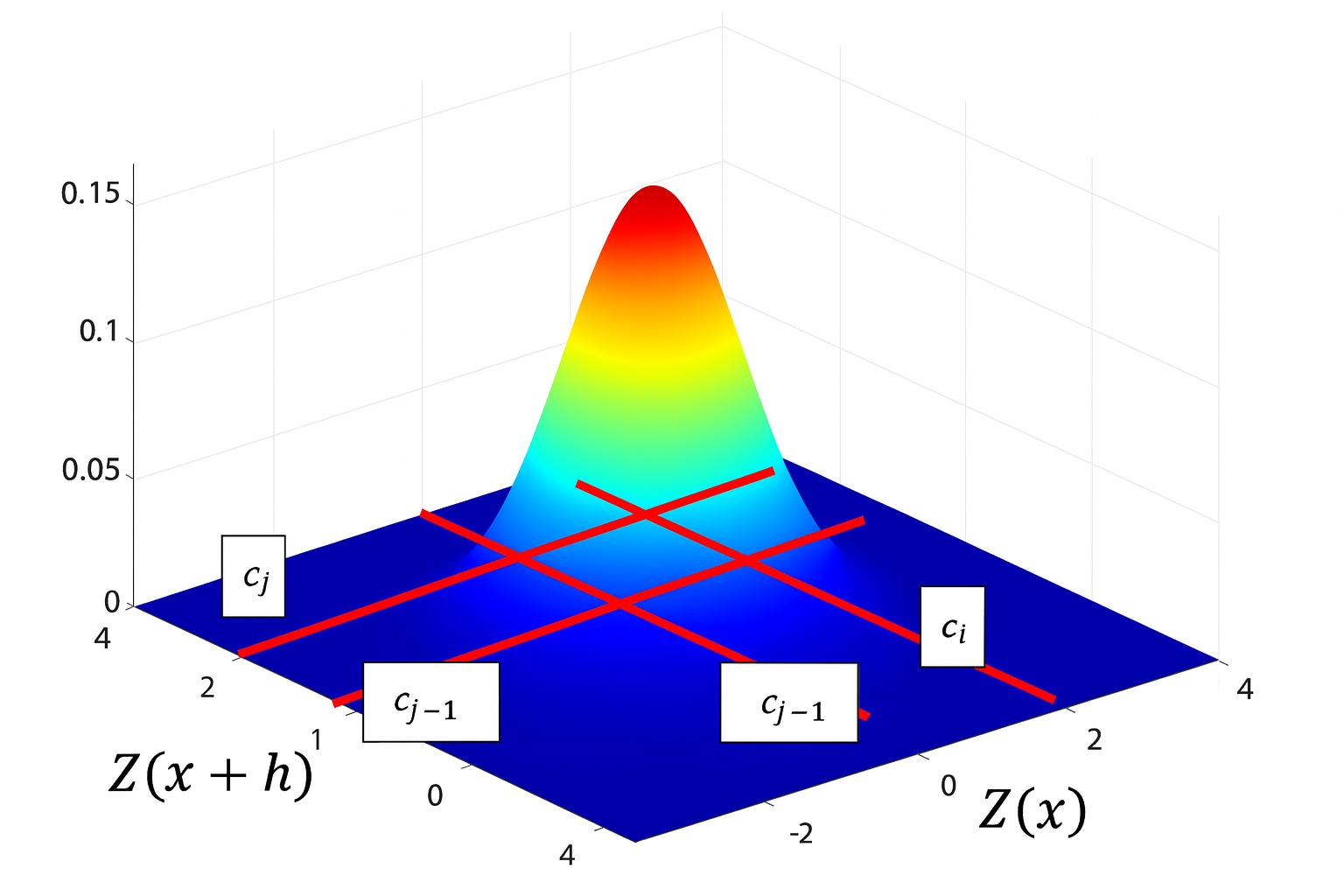
Figure 4:Probabilité des .
Comment tenir compte des faciès observés aux points échantillons (quelles valeurs gaussiennes simuler aux points échantillons)?¶
Pour tenir compte des faciès observés aux points échantillons dans la méthode TGS, on utilise un échantillonnage de Gibbs. L’échantillonnage de Gibbs est une méthode de Monte-Carlo par chaînes de Markov (MCMC) qui permet d’échantillonner une distribution complexe en construisant une chaîne de Markov dont la loi stationnaire est précisément la distribution cible. Étant donnée une distribution de probabilité sur un espace , l’algorithme génère une suite d’échantillons dont la distribution limite est , ce qui permet de tirer aléatoirement un élément de selon la loi souhaitée.
Dans le contexte de la TGS, l’échantillonnage de Gibbs est nécessaire car les valeurs latentes ne sont pas directement observables : seules les catégories , issues de la troncature du champ latent, sont connues. Le principe repose sur le fait que chaque faciès correspond à un intervalle de troncature . Ainsi, si le point appartient au faciès , alors la valeur latente associée doit obligatoirement vérifier :
L’objectif du Gibbs est donc d’échantillonner, pour chaque point où un faciès est observé, une valeur latente compatible à la fois avec la fonction de covariance et avec les contraintes de troncature imposées par les faciès observés.
L’algorithme d’échantillonnage de Gibbs pour le conditionnement du champ latent repose sur une application successive du krigeage simple, lequel, rappelons-le, permet d’obtenir la distribution statistique conditionnelle d’une variable gaussienne en un point donné. À chaque itération, on met à jour une valeur latente en utilisant toutes les autres valeurs déjà fixées. Les itérations du Gibbs s’effectuent alors comme suit :
Initialisation.
Pour chaque point échantillonné , choisir aléatoirement une valeur gaussienne dans l’intervalle correspondant au faciès observé, c’est-à-dire :
Cette initialisation respecte donc le codage.
1. Sélection d’un point.
Choisir un point aléatoirement parmi les points à conditionner. Retirer temporairement la valeur courante du système.
2. Estimation de la loi conditionnelle.
Estimer la distribution conditionnelle de , compte tenu de toutes les autres valeurs latentes restantes :
où proviennent du krigeage simple.
3. Échantillonnage tronqué.
Étant donné que , tirer une nouvelle valeur de à partir de la loi normale tronquée à l’intervalle imposé par le patron de codage :
4. Mise à jour.
Remplacer l’ancienne valeur de par la nouvelle valeur tirée.
5. Critère d’arrêt.
Vérifier un critère de convergence (nombre d’itérations, stabilité des moments, autocorrélation).
Si le critère est satisfait : arrêter.
Sinon : retourner à l’étape 1.
À la fin de multiple itération, nous nous retrouvons avec des valeurs gaussiennes corrélé selon et respectant les seuils. Ainsi, l’échantillonnage de Gibbs permet de générer un champ latent qui respecte simultanément la structure spatiale gaussienne imposée par le variogramme et les informations catégorielles observées via les intervalles du patron de codage.
Simulations Plurigaussiennes¶
Le modèle plurigaussien étend le modèle gaussien tronqué en utilisant plusieurs variables gaussiennes corrélées pour modéliser des faciès avec des relations spatiales plus complexes. Par simpliciter, nous verrons que le cas avec deux champs latents. On peut résumer l’algorithme par :
Simulation de deux champs gaussiens avec une fonction de covariance
Simuler deux variables gaussiennes et respectant la matrice de covariance .
Chaque champ possède son propre modèle de variogramme direct, et les deux champs peuvent être corrélés entre eux via les covariances croisées et .Définition du plan de codage des faciès
Associer chaque faciès à une zone (rectangle ou autre forme) du plan .
Ce plan encode les relations spatiales souhaitées (exclusions, transitions obligatoires, voisinages imposés).
Les proportions des faciès sont déterminées par l’intégrale de la densité gaussienne bivariée sur les zones définies.Inférence des paramètres
Calculer les covariances expérimentales des indicatrices ainsi que leurs covariances croisées.
Ajuster ensuite les modèles de covariance des deux champs latents et leur corrélation afin de reproduire au mieux les structures spatiales observées dans les données.Conditionnement aux données observées : échantillonneur de Gibbs
Pour chaque point d’observation , on applique un échantillonnage de Gibbs, où la loi conditionnelle de est obtenue par cokrigeage simple conditionnellement aux valeurs latentes déjà fixées :calculer la distribution normale conjointe conditionnelle par cokrigeage simple ;
tirer une paire dans cette loi conditionnelle ;
vérifier que cette paire appartient à la zone du plan correspondant au faciès observé ;
sinon, répéter le tirage jusqu’à obtenir une paire compatible ;
mettre à jour la valeur latente et passer au point suivant ;
Ce balayage est répété jusqu’à stabilisation (convergence du Gibbs).
Simulation conditionnelle finale
Réaliser une simulation gaussienne conditionnelle complète pour les champs et en utilisant les valeurs obtenues lors du conditionnement.
Convertir ensuite le résultat en faciès à l’aide du plan de codage.
La Fig. 5 présente un exemple de patron de codage complexe. Par exemple, si l’on observe les valeurs latentes et , le couple tombe dans le rectangle associé au faciès , et celui-ci est donc attribué. La Fig. 6 illustre l’application de ce patron de codage à deux champs gaussiens indépendants. Le champ latent suit un variogramme sphérique isotrope de portée 150 pixels, tandis que le champ latent suit un variogramme sphérique isotrope de portée 260 pixels. Le domaine simulé couvre une grille de 500 × 500 pixels.
On constate que les relations spatiales entre les faciès générés sont très complexes, mais certaines structures sont clairement imposées par le patron de codage : le faciès est entièrement contenu dans , tandis que les faciès , et baignent dans et ne peuvent donc jamais entrer en contact direct les uns avec les autres.
La Fig. 7 présente quatre images : une image réelle aux rayons X montrant les pores d’un grès, ainsi que trois réalisations PGS générées pour reproduire cette structure. Selon vous, laquelle correspond à l’image réelle ? Il s’agit de celle située en haut à gauche. Les simulations sont suffisamment réalistes pour rendre la distinction non triviale voir impossible.
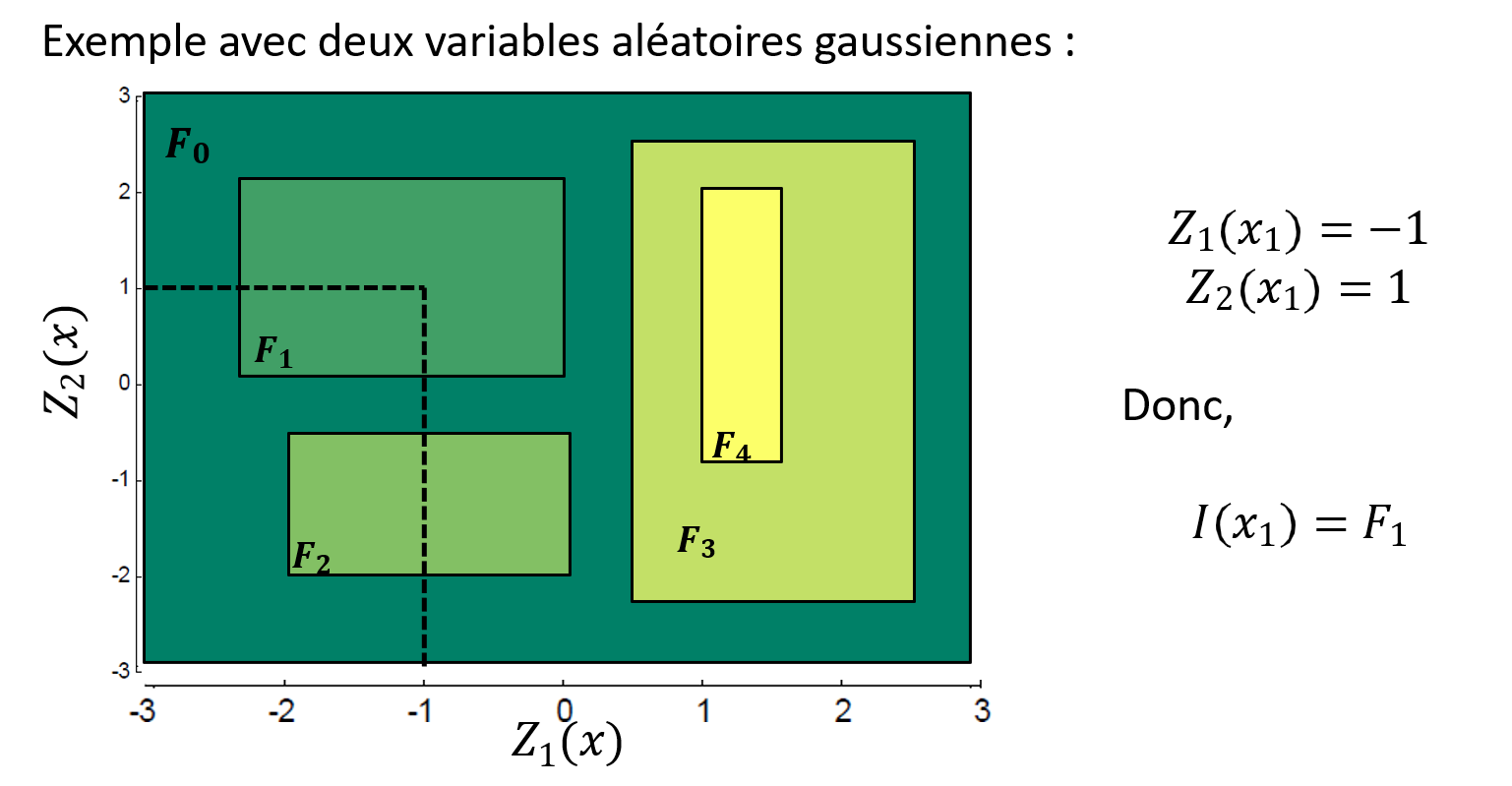
Figure 5:Exemple de plan de codage utilisé pour une simulation plurigaussienne à deux champs latents.
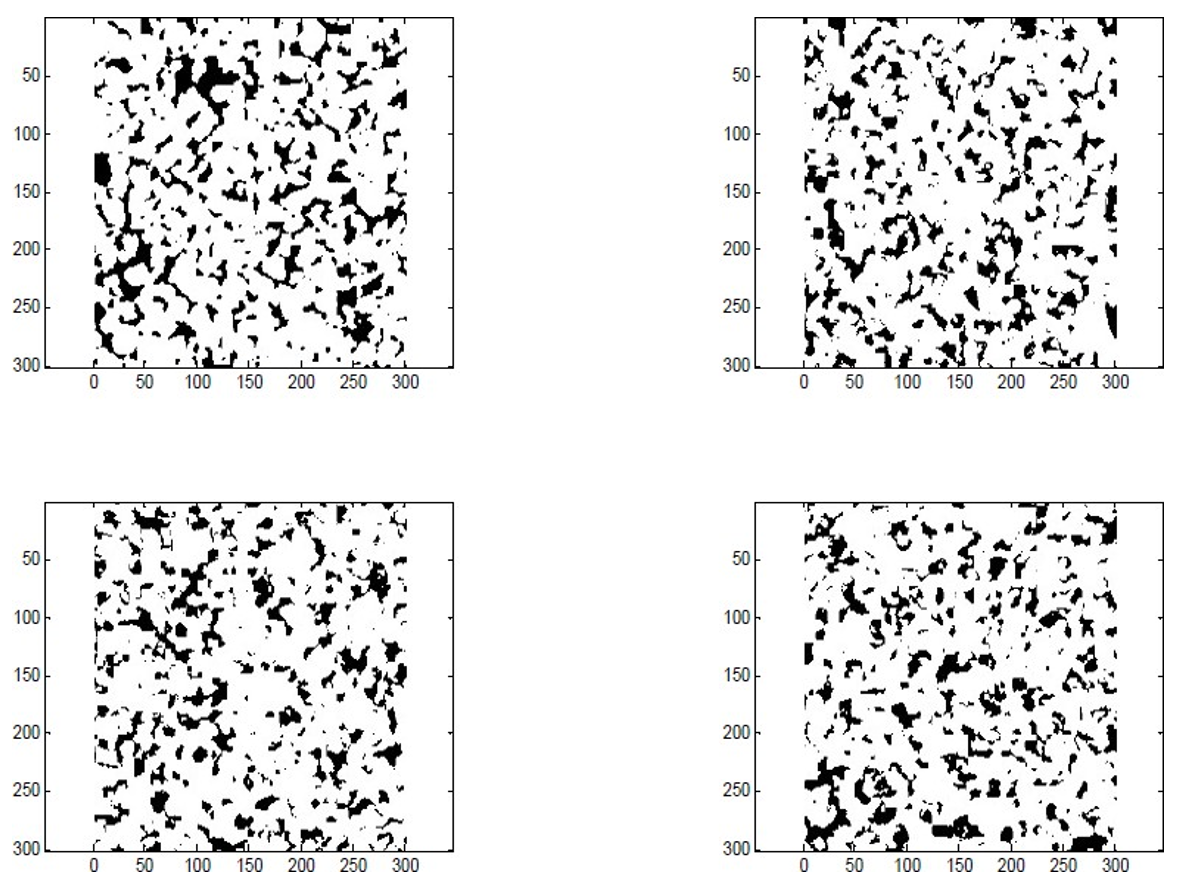
Figure 6:Exemple de simulation plurigaussienne réalisée à partir de deux champs latents gaussiens non corrélés, suivant respectivement des variogrammes sphérique isotrope de portées de 150 pixels et 260 pixels, sur une grille de 500 par 500 pixels.

Figure 7:Une image aux rayons X montrant les pores d’un grès, accompagnée de trois réalisations plurigaussiennes (PGS). Selon vous, laquelle correspond à l’image réelle ?