Les méthodes de simulation multipoints ( Multiple Point Statistic, MPS) ont été développées pour surmonter les limites fondamentales des approches géostatistiques classiques fondées uniquement sur le variogramme. En effet, un variogramme ne décrit que des relations bivariées (entre deux points), ce qui est insuffisant pour représenter des structures géologiques complexes telles que les chenaux sinueux, les veines discontinues, les réseaux de fractures, les figures polygonales, ou encore les motifs hiérarchiques présents dans de nombreux environnements sédimentaires et structuraux.
Une image classique et largement utilisée pour illustrer cette idée est celle présentée dans Caers and Zhang (2004). La Fig. 1 en montre un exemple. On constate trois contexte géologique bien différent, cependant leur variogramme expérimentales dans les deux directions principales sont très similaires. On constante bien que le variogramme ne permet par de distinguer les structures spatiales entre les images.
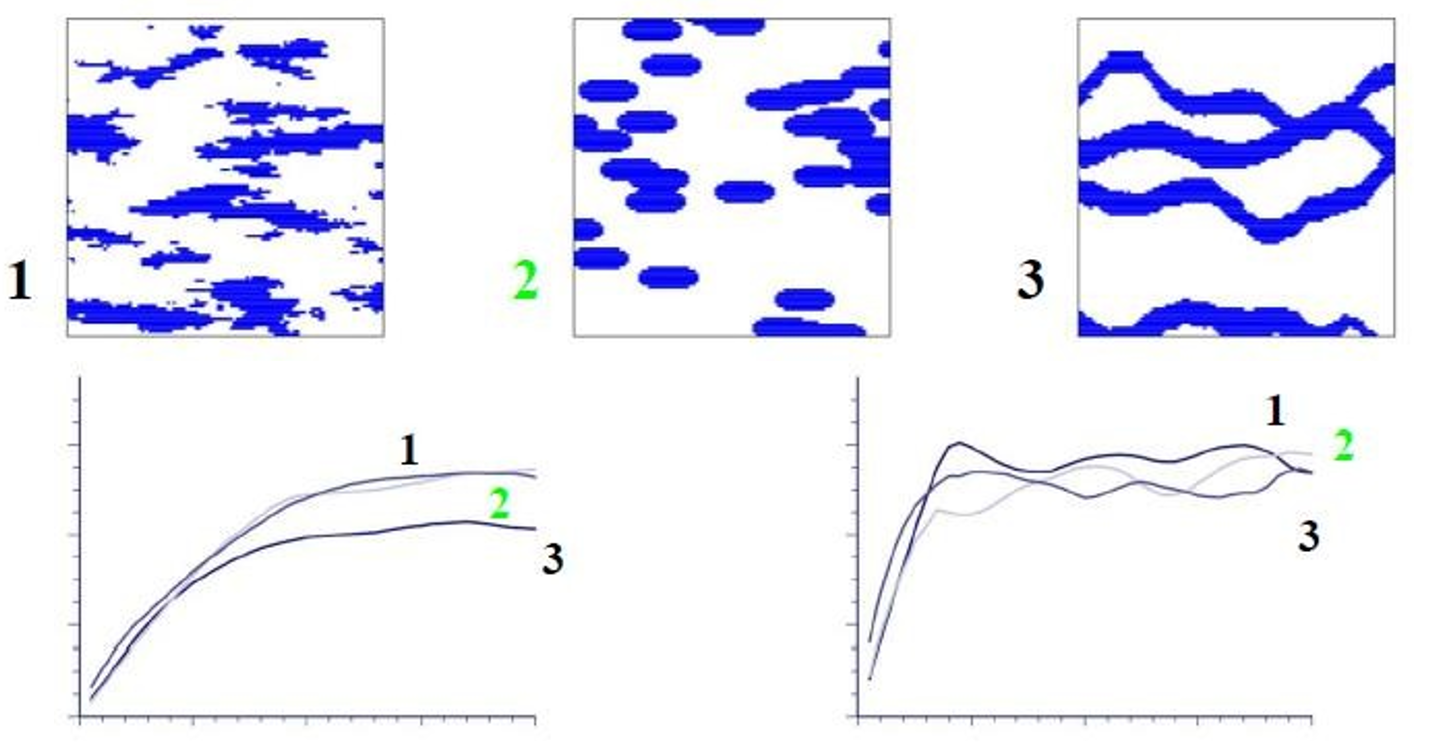
Figure 1:Comparaison des variogrammes expérimentaux obtenus pour trois champs de faciès présentant des structures spatiales clairement distinctes.
Les méthodes MPS permettent au contraire de capturer des motifs géométriques, topologiques et structuraux en utilisant une image d’entraînement (training image), qui joue le rôle d’un modèle conceptuel. Cette image encode des informations de haute dimension (patterns), impossibles à déduire avec les seuls outils basés sur la covariance.
Ainsi, les méthodes multipoints sont particulièrement utiles lorsque :
les faciès présentent des géométries non gaussiennes, non linéaires ou discontinues ;
les structures ne peuvent pas être décrites par un variogramme (ou seraient mal reproduites par celui-ci) ;
les relations spatiales entre éléments géologiques nécessitent plus que des transitions locales ;
aucun modèle analytique simple ne permet de représenter l’organisation spatiale observée.
L’idée de base : copier un dessin de référence¶
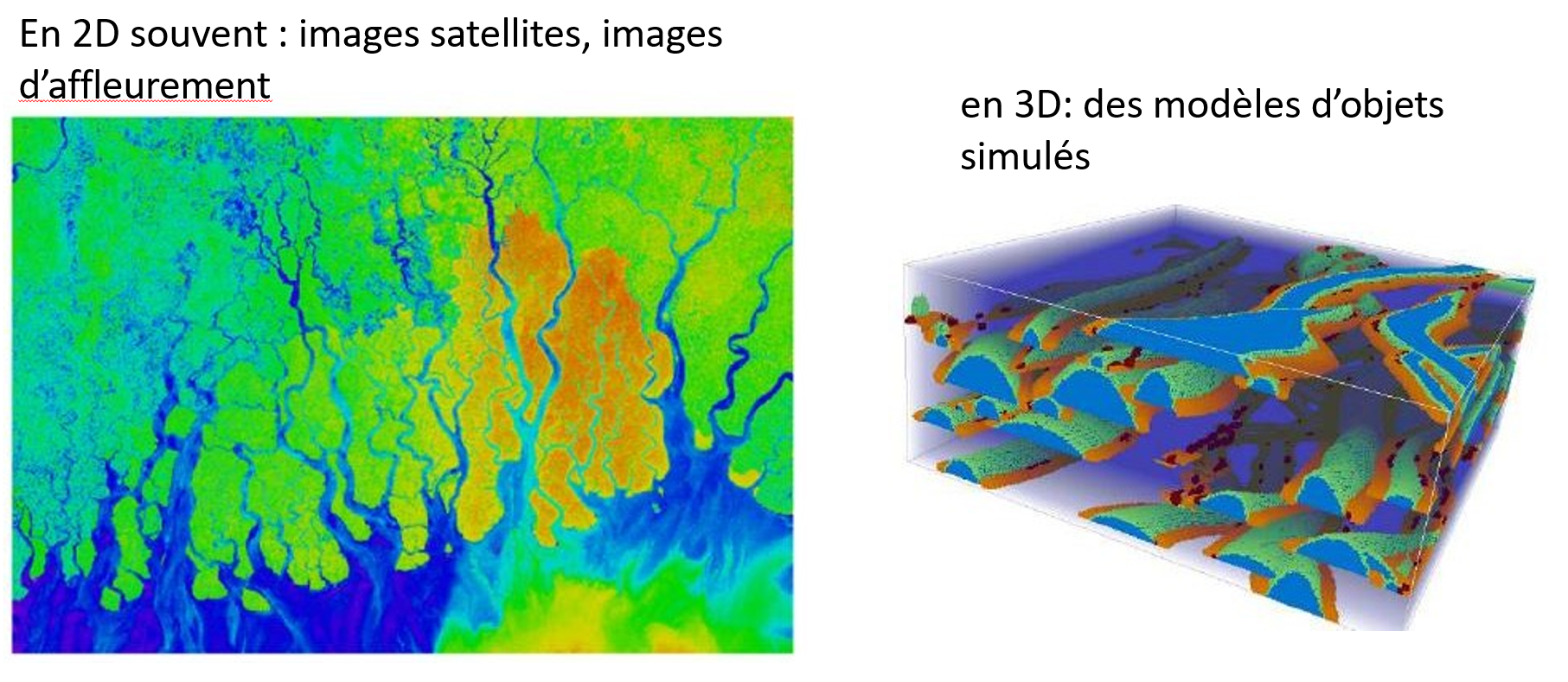
Les méthodes multipoints utilisent un modèle analogue, c’est-à-dire un exemple d’image (ou de carte) qui ressemble à ce qu’on imagine dans le sous-sol : un dessin, une carte géologique, une photo satellite ou même une simulation d’objets. Ce modèle sert de modèle à copier. Il s’agit de l’image d’entraînement (training image, TI).
On va ensuite “dessiner” la simulation, point par point ou par blocs, en veillant à rester cohérent avec l’image d’entraînement (TI). L’idée ressemble à celle de reconstruire un nouveau casse-tête à partir d’un casse-tête déjà complété : on s’inspire en permanence des motifs présents dans la TI pour assembler progressivement un modèle qui en reproduit la structure spatiale.
Méthode 1 : la simulation point par point (pixel par pixel)¶
La simulation multipoints point par point consiste à construire le modèle simulé de manière séquentielle, un emplacement à la fois, en exploitant l’information déjà simulée dans un voisinage local. À chaque nouveau point à simuler, on utilise la configuration (ou pattern) déjà présente autour de ce point pour identifier, dans l’image d’entraînement (TI), les motifs similaires. Cette recherche permet d’établir une distribution conditionnelle empirique pour la catégorie à simuler.
Le processus peut être décrit comme suit :
Initialisation du modèle
Le champ simulé est initialisé avec des valeurs connues (données observées) et des cellules encore non simulées.Définition du voisinage de simulation
Pour un point non simulé, on considère un voisinage structuré (fenêtre ou gabarit) contenant les valeurs déjà simulées et utilisées comme condition.Recherche de motifs similaires dans la TI
Le voisinage partiellement renseigné est comparé à toutes les occurrences similaires dans la TI.
On identifie ainsi l’ensemble des positions de la TI où le motif correspond (exactement ou dans une certaine tolérance).Construction de la distribution conditionnelle
À partir des occurrences identifiées, on extrait la catégorie présente dans la TI au centre du motif.
La distribution des catégories possibles constitue alors une approximation empirique de la loi conditionnelle multipoints.Attribution d’une catégorie
Une catégorie est tirée aléatoirement selon cette distribution empirique, puis affectée au point en cours de simulation.Répétition séquentielle
Le processus est répété pour tous les points du domaine, selon un chemin de visite (souvent aléatoire), jusqu’à ce que la grille complète soit simulée.
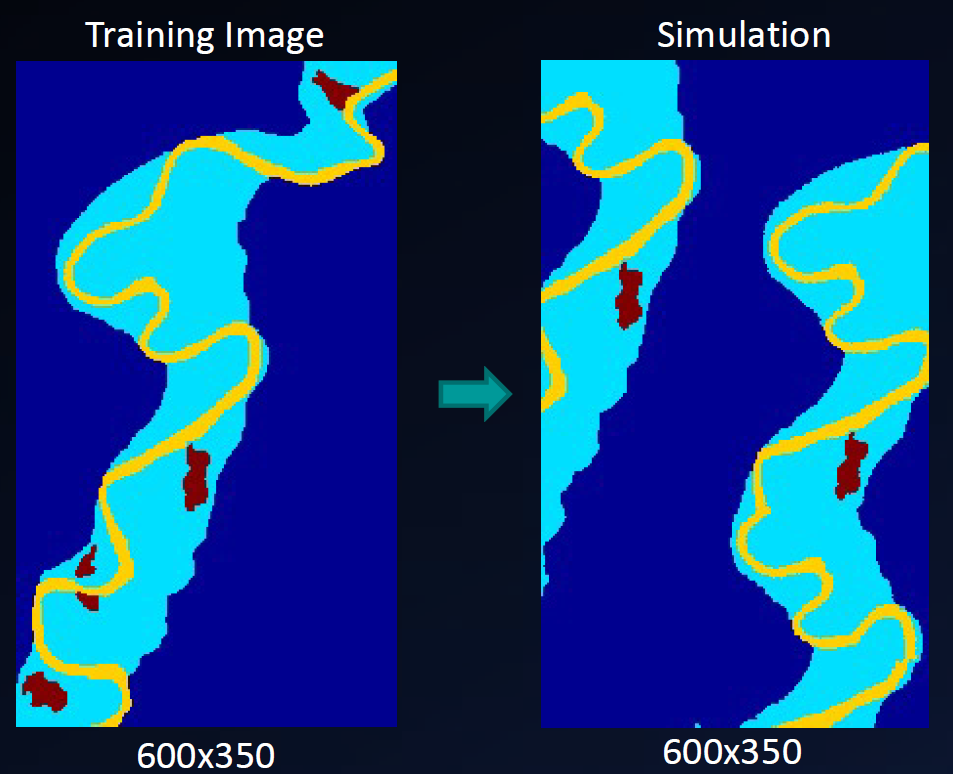
La Fig. 2 illustre un exemple simple de la méthode multipoint pixel par pixel. Dans cet exemple, on souhaite simuler le faciès situé dans le carré rouge. Pour ce faire, on recherche dans la TI les occurrences où la même configuration de trois faciès déjà simulés apparaît autour d’un point donné. On observe dans la TI qu’une telle configuration existe et qu’elle correspond à un faciès bleu au centre. En analysant l’ensemble des occurrences similaires dans la TI, on obtient une distribution conditionnelle : 29 % de faciès bleu et 71 % de faciès jaune, et aucune occurrence du faciès vert. Le faciès du point à simuler est alors tiré aléatoirement selon cette distribution conditionnelle, ce qui détermine la catégorie attribuée au pixel encadré en rouge.
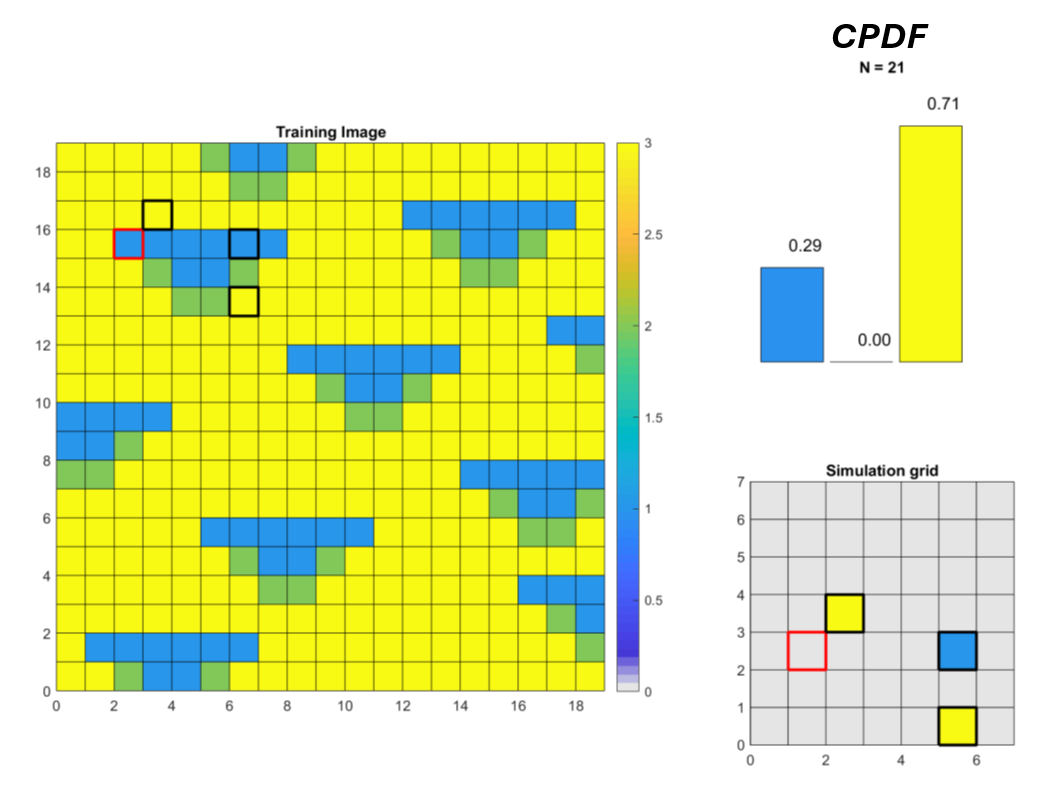
Figure 2:Schématisation de la méthode multipoint pixel par pixel utilisée dans l’algorithme SNESIM.
La méthode pixel par pixel repose sur la capacité de la TI à fournir suffisamment d’exemples pour représenter les motifs de voisinage rencontrés durant la simulation. Lorsque le motif recherché est absent ou trop rare dans la TI, deux stratégies sont généralement utilisées :
Réduire la taille du voisinage afin d’augmenter la probabilité de trouver des occurrences compatibles (perte d’information contextuelle).
Autoriser des correspondances approximatives (distance de similarité non nulle), au prix d’un compromis entre fidélité géologique et robustesse algorithmique.
Cette approche est conceptuellement simple et constitue la base de méthodes telles que SNESIM, mais elle peut devenir coûteuse en calcul lorsque la TI est large ou lorsque les motifs recherchés sont rares. Dans ce cas, on adopte l’algorithme du Direct Sampling, qui permet d’accélérer les calculs.
Méthode 2 : Simulation par morceaux (patch-based simulation)¶
La simulation multipoints par morceaux consiste à reproduire des structures spatiales en copiant-collant des blocs (patchs) extraits de la TI, plutôt que de simuler pixel par pixel. Cette approche est adaptée aux objets géologiques présentant des formes continues ou des textures complexes difficiles à générer avec une méthode point par point. La méthodologie est la suivante :
Définition d’un ensemble de patchs On extrait dans la TI des blocs de taille fixe (par exemple 8×8 ou 16×16 pixels), qui serviront de motifs de référence.
Caractérisation des patchs Chaque patch est décrit au moyen de mesures spatiales (textures, gradients, statistiques locales), afin de faciliter la comparaison entre patchs (Fig. 3).
Regroupement des patchs Les patchs similaires sont regroupés (clustering) pour accélérer la recherche de motifs compatibles durant la simulation.
Simulation par collage adaptatif Lors du remplissage de la grille simulée :
on compare le voisinage déjà simulé avec les patchs candidats ;
on sélectionne le patch minimisant une mesure de dissimilarité ;
on colle le patch à l’emplacement courant en conservant les pixels déjà simulés.
Gestion du recouvrement Pour éviter des artefacts visibles aux frontières des patchs, certaines variantes utilisent :
des zones de transition lissées,
un chemin de coupure optimal (méthode image quilting),
ou une fusion statistique locale.
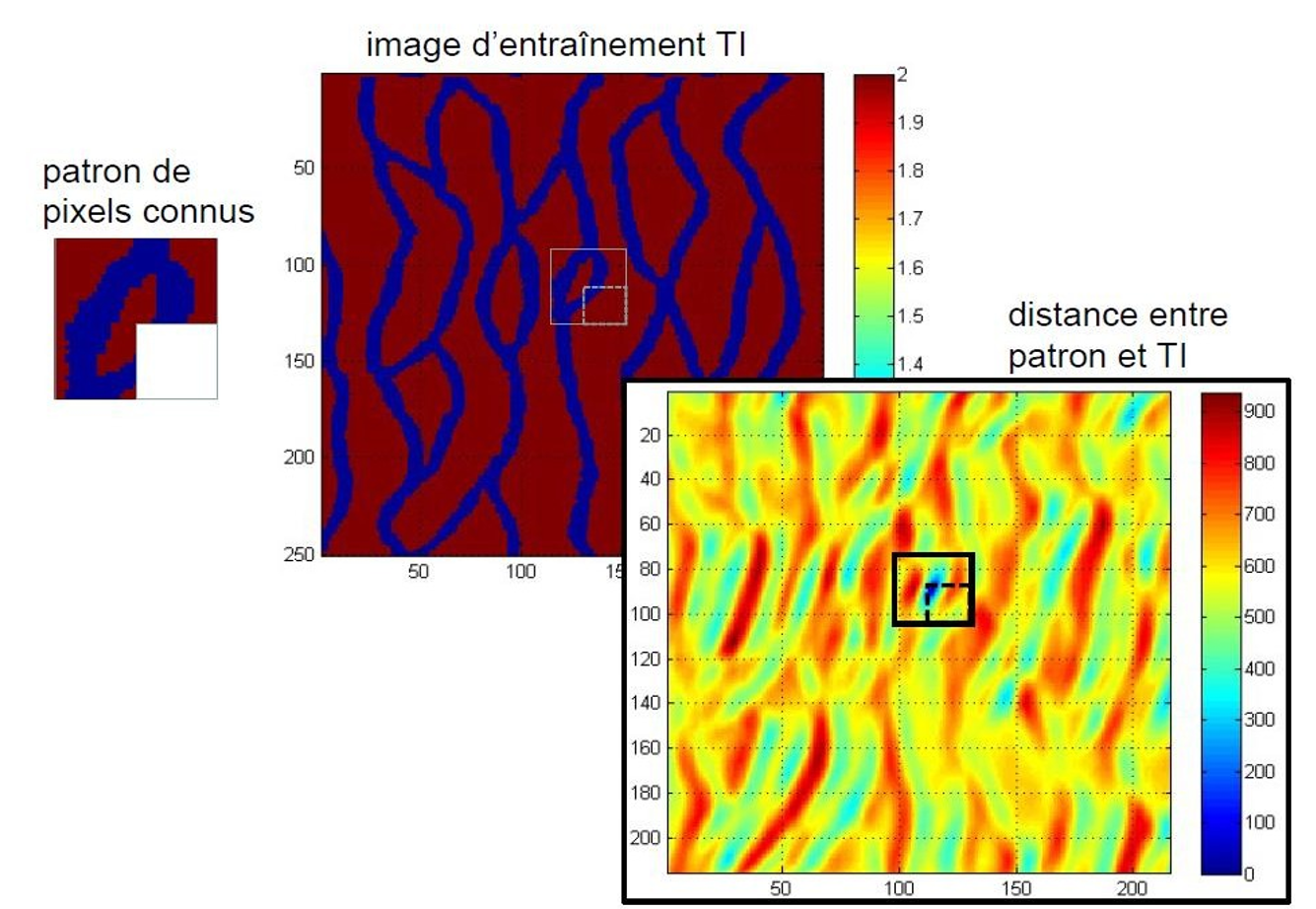
Figure 3:Exemple de mesure de la distance entre un patch et la TI.
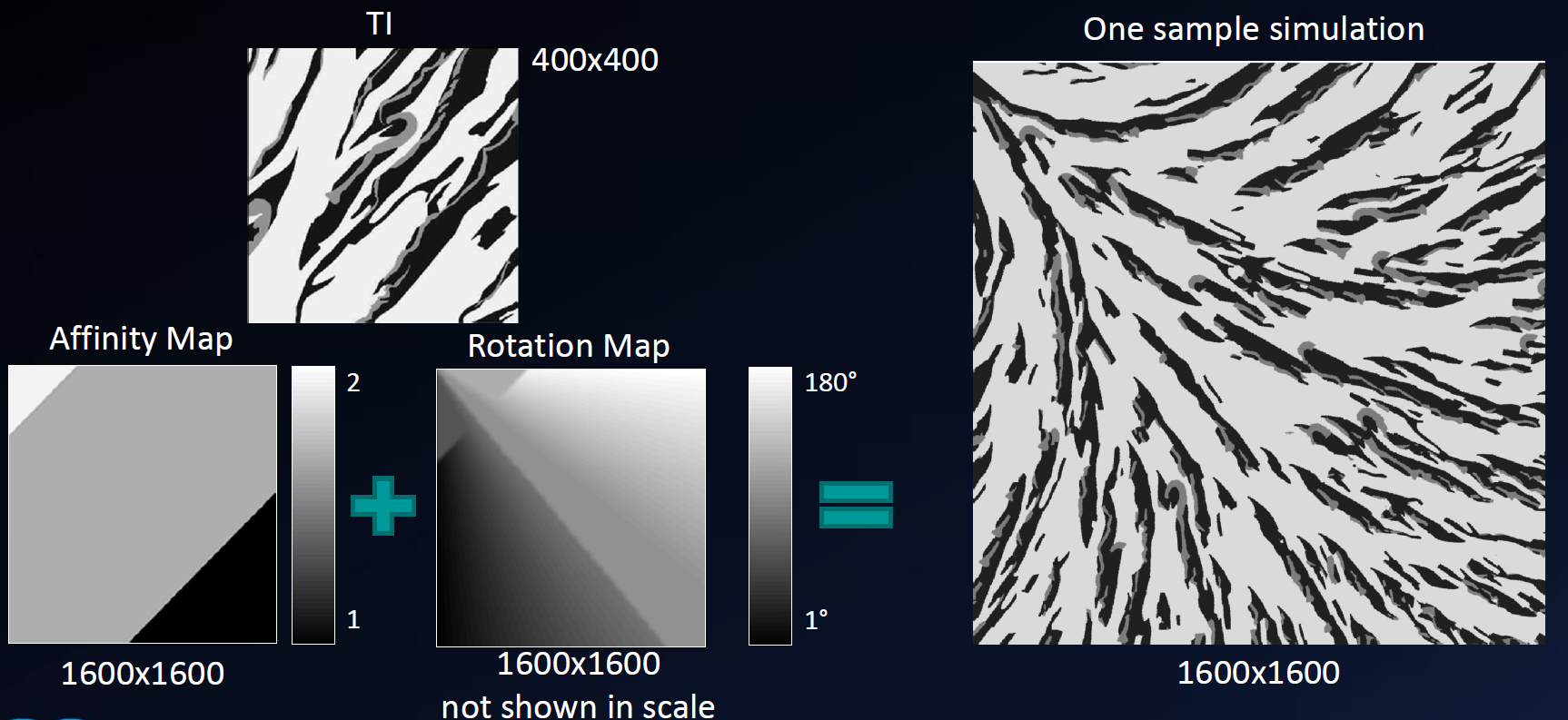
Les méthodes de simulation par patchs présentent plusieurs avantages importants (Fig. 4). Elles permettent d’abord une reproduction très fidèle des motifs structuraux présents dans la TI, ce qui en fait un outil particulièrement efficace pour représenter des géométries géologiques complexes. Elles offrent également une grande robustesse pour modéliser des architectures de grande échelle, où la continuité spatiale des objets joue un rôle essentiel. De plus, ces approches sont bien adaptées à la représentation de textures non stationnaires ou multi-échelles, car les patchs capturent directement les variations locales de structure présentes dans la TI.
Cependant, ces méthodes comportent aussi une limite notable : des discontinuités peuvent apparaître aux jonctions entre patchs si la fusion n’est pas optimale. La qualité de la transition dépend fortement de la taille des patchs, de leur degré de similarité avec le voisinage simulé, ainsi que de la technique de couture employée. Une fusion inadéquate peut ainsi entraîner des “coutures” visibles, réduisant le réalisme de la simulation.

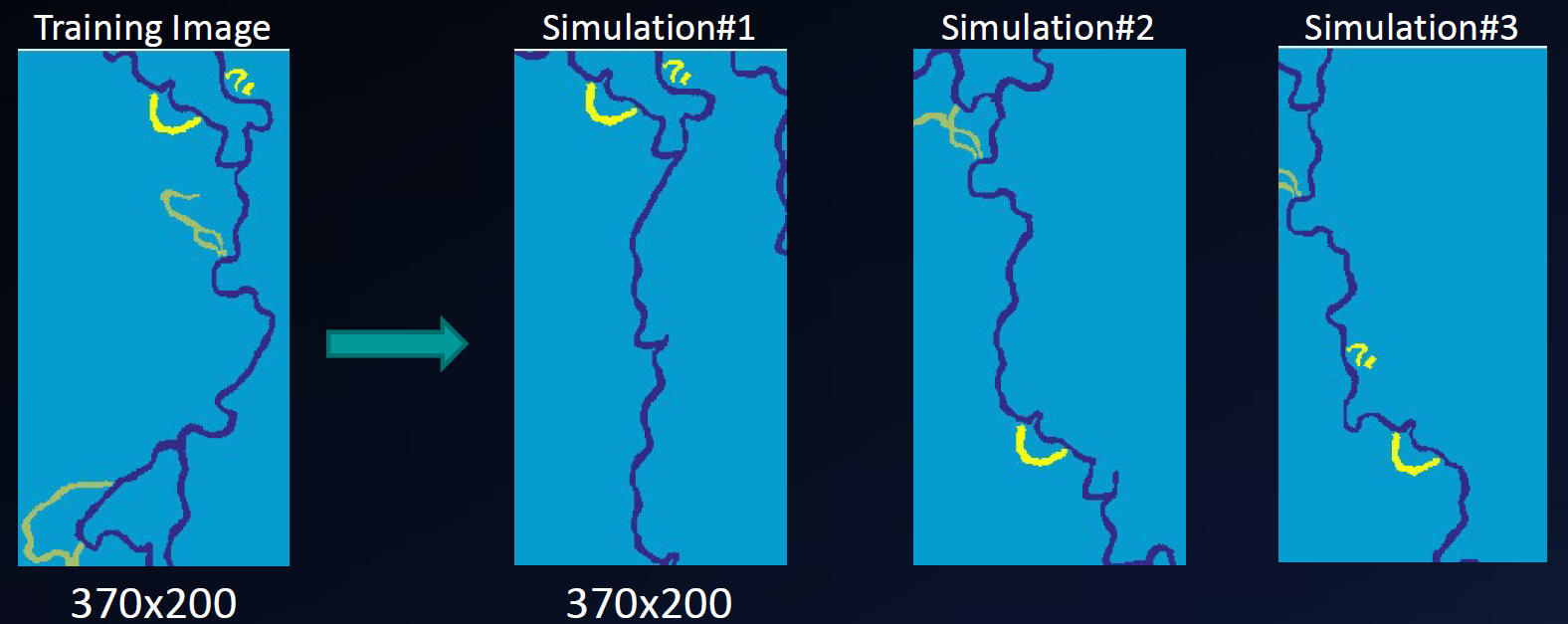
Figure 4:Exemple de l’application d’un algorithme de simulation par patch.
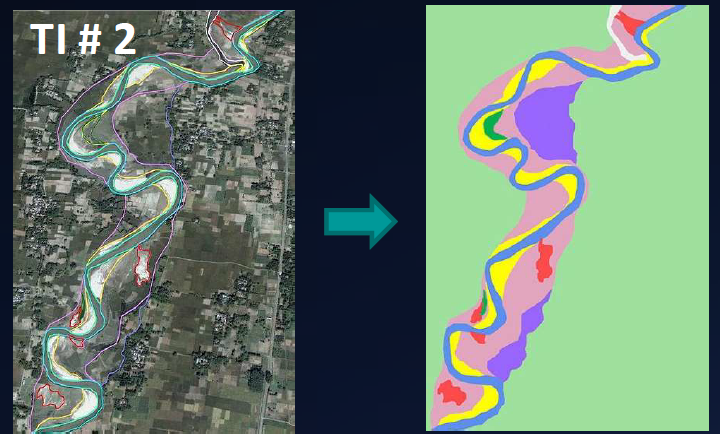
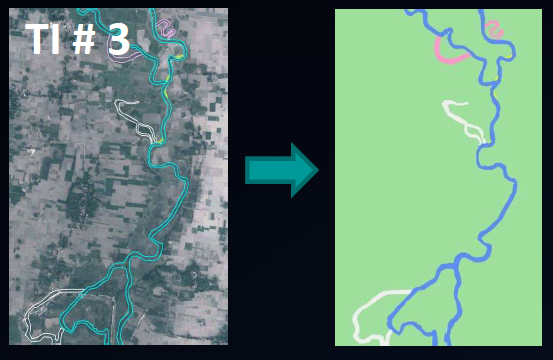
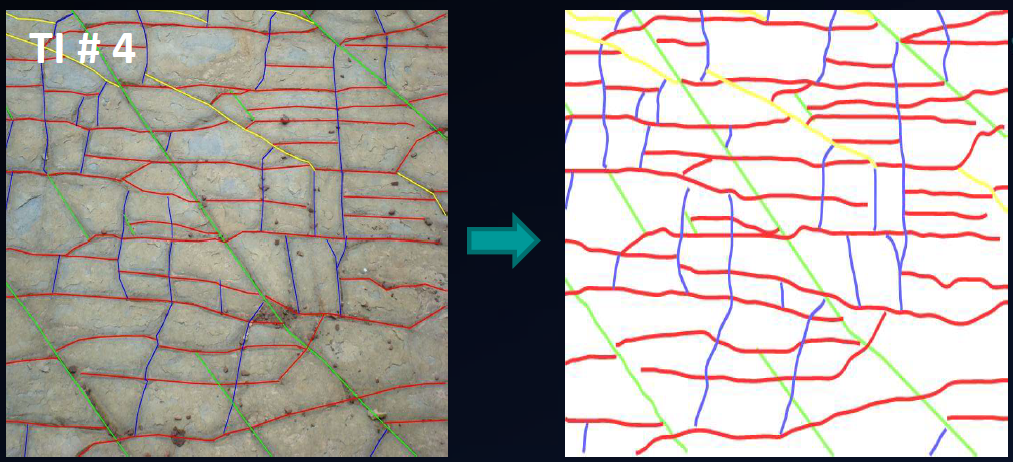
Exemple d’image d’entrainement et de réalisation¶
Cette section présente une série de TIs et de simulations obtenues par MPS. Constatez la grande versatilité et l’efficacité des méthodes MPS.