Abstract¶
Dans ce chapitre, nous explorons comment la géostatistique permet de travailler avec plusieurs variables à la fois, par exemple lorsqu’on dispose de mesures directes (comme la teneur en Ni d’un gisement) et de données indirectes (comme des levées géophysiques). Nous verrons d’abord ce qu’est le cokrigeage, une extension naturelle du krigeage, qui vise à mieux estimer une variable principale en tirant parti de l’information contenue dans d’autres variables secondaires corrélées à la variable principale. Pour y arriver, nous apprendrons à calculer expérimentalement des covariances et des variogrammes croisés, qui mesurent comment deux variables distinctes évoluent l’une par rapport à l’autre en fonction de la distance. Nous présenterons ensuite le modèle linéaire de corégionalisation, le plus utilisé dans le domaine de la géostatistique multivariable pour modéliser les structures spatiales entre une variable principale et des variables secondaires. Vous verrez les conditions d’admissibilité de ce modèle mathématique. Enfin, nous discuterons de situations concrètes où le cokrigeage est utile : quand il améliore la précision, quand le gain est négligeable, et comment le vérifier à l’aide de méthodes de validation croisée adaptées au contexte multivarié. L’objectif est de vous donner les outils pour choisir judicieusement entre un krigeage et un cokrigeage, en comprenant les avantages et les limites de chaque approche.
Introduction¶
Dans de nombreuses situations, plusieurs variables sont mesurées, soit aux mêmes points d’échantillonnage, soit à des points d’échantillonnage distincts. Par exemple, on peut connaître précisément la position du sommet d’un réservoir pétrolier à partir d’observations de quelques forages, tout en disposant d’une couverture sismique étendue fournissant une estimation plus approximative de cette position. Dans un gisement de cuivre (Cu) et de nickel (Ni), les teneurs de ces deux métaux peuvent être mesurées à chaque point de mesure et pourraient présenter une forte corrélation. En hydrogéologie, il est courant de disposer de mesures de charges hydrauliques à certains points et de transmissivités à un nombre plus restreint d’autres points.
Pour exploiter au mieux ces informations, on considère généralement qu’une variable est prioritaire, appelée la variable principale , tandis que les autres sont considérées comme secondaires. Afin de simplifier le développement des équations, nous supposerons qu’il n’y a qu’une seule variable secondaire . L’extension à plusieurs variables secondaires s’effectue directement et ne pose pas de difficultés théoriques particulières.
La question centrale est donc : comment tirer parti de l’information fournie par la variable secondaire pour améliorer l’estimation de la variable principale ? La démarche suivie constitue une généralisation naturelle de celle présentée dans le chapitre consacré au krigeage.
Mise en contexte sur un cas synthétique¶
Supposons que l’on ait observé une variable principale sur une grille régulière de 100 m × 100 m, avec un échantillon tous les 10 m dans les deux directions principales. Cela correspond à un total de 100 observations. Par ailleurs, supposons que l’on dispose d’une levée géophysique couvrant l’ensemble de la grille. La Fig. 1 illustre ce type de configuration et la Fig. 2 présente la corrélation entre les paires de points colocalisés, c’est-à-dire lorsque l’on mesure simultanément la variable principale et la secondaire à la même localisation. On constate une certaine corrélation entre les deux variables. De plus, on a beaucoup plus d’observations des variables secondaires que des variables principales. Il serait alors intéressant d’utiliser des informations (une bonne corrélation et plusieurs données secondaires) pour améliorer l’estimation de la variable principale.
Il est alors légitime de se demander : la variable secondaire nous apportera-t-elle réellement des informations supplémentaires sur la variable principale ? Nous verrons prochainement que les calculs associés au cokrigeage sont plus lourds numériquement et peuvent entraîner des problèmes d’admissibilité du modèle théorique. Il est donc primordial de ne se lancer dans cette tâche que si l’on est convaincu que le gain attendu en vaut la peine. Nous aborderons ces notions au cours de la lecture.
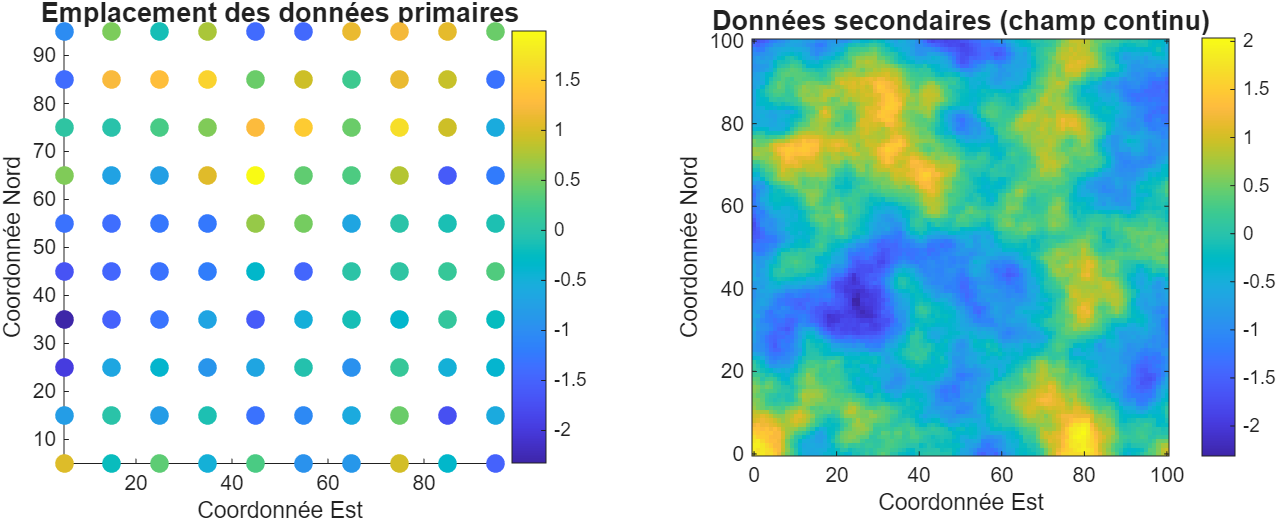
Figure 1:Exemple de données multivariables. La variable principale est observée à un nombre limité d’emplacements, tandis que la variable secondaire est présente à tous les points.
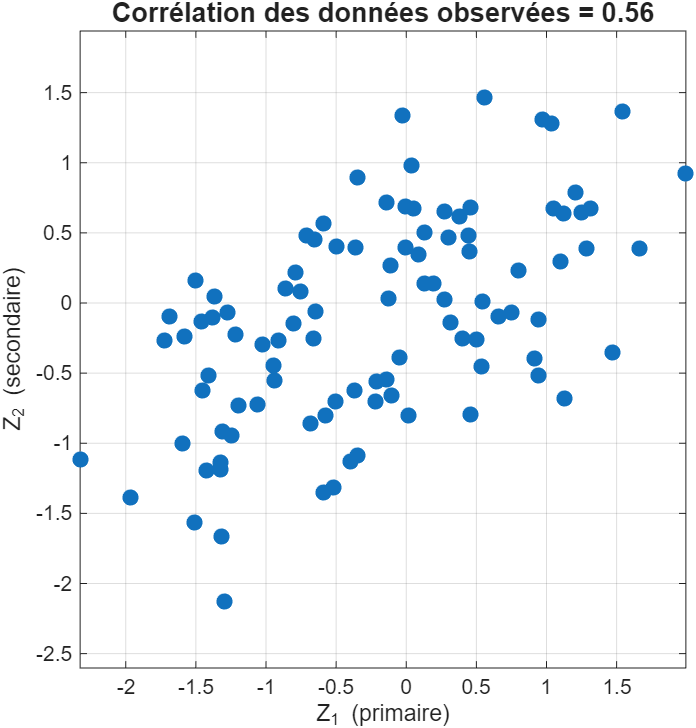
Figure 2:Exemple de données multivariables. Nuage de points des données observées et de leur corrélation.