Le krigeage, présenté au chapitre 8, est une méthode d’estimation spatiale qui s’appuie sur la continuité d’une variable unique. Toutefois, dans de nombreuses applications, plusieurs variables corrélées sont mesurées, parfois aux mêmes emplacements, parfois séparément. Cette corrélation peut être mise à profit pour améliorer les estimations.
Le cokrigeage constitue une extension naturelle du krigeage au cas multivariable. Il combine l’information de la variable principale avec celle d’une ou plusieurs variables secondaires pour raffiner l’estimation de la variable d’intérêt. Cette approche repose sur les variogrammes et covariances croisées entre variables et nécessite la résolution d’un système plus complexe, mais offrant une information plus complète.
Ce chapitre présente les principes fondamentaux du cokrigeage, les formulations du cokrigeage ordinaire (CO) et du cokrigeage simple (CS), ainsi que les conditions pour obtenir un estimateur sans biais.
Variance d’estimation¶
Dans le cadre du cokrigeage, l’estimateur linéaire de la variable principale est construit à partir des observations de et de celles d’une variable secondaire . La variance de l’erreur, ou variance d’estimation, quantifie l’incertitude associée à cette estimation en tenant compte de toutes les sources d’information disponibles. Ainsi, la valeur estimée à un point d’intérêt dépend à la fois des observations de la variable principale et de celles de la variable secondaire, pondérées en fonction de leurs corrélations spatiales directes et croisées.
Soit l’estimation de au point , donnée par :
où et représentent respectivement les poids appliqués aux observations de la variable principale et de celles de la variable secondaire .
Remarque :
Nous utilisons deux indices distincts pour souligner que les coordonnées des observations de et de peuvent différer.
Autrement dit, les données peuvent être :
Colocalisées : chaque point de mesure possède à la fois une observation de et de ;
Non colocalisées : aucune observation des deux variables n’est disponible au même emplacement ;
Partiellement colocalisées : certaines positions présentent les deux variables, tandis que d’autres n’en présentent qu’une seule.
La Fig. 1 illustre ces trois cas de figure. Par simplification, nous adopterons une nomenclature unifiée pour représenter l’ensemble des cas. Ainsi, désignera la observation de la variable principale , et la observation de la variable secondaire . Il est important de noter que les ensembles d’observations de et de peuvent différer, tant en nombre qu’en position spatiale. Ainsi, l’indice fait référence à la position de l’observation dans l’ensemble des données de chaque variable, et non à une position commune dans l’espace. Autrement dit, la localisation associée à n’est pas nécessairement la même que celle de . Pour alléger la notation, nous omettrons explicitement les indices de position et écrirons simplement au lieu de , et de même au lieu de .
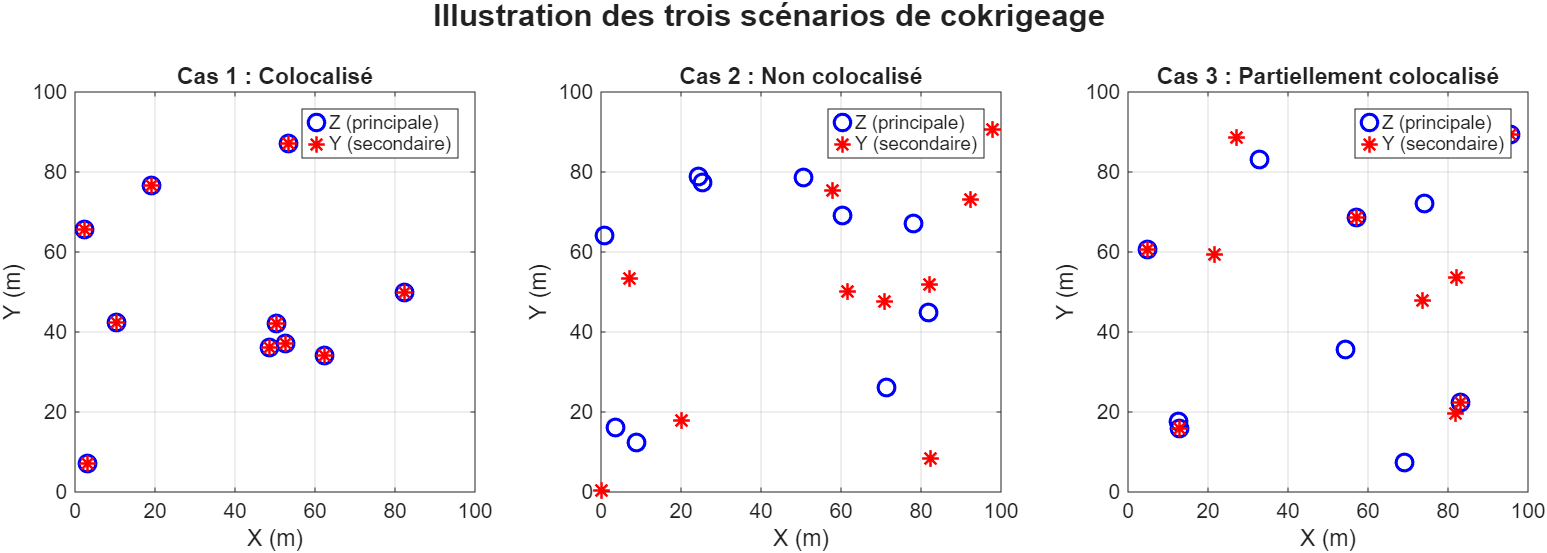
Figure 1:Illustration de trois configurations de données entre la variable principale (ronds bleus) et la variable secondaire (étoiles rouges).
Ainsi, la variance d’estimation s’exprime alors comme :
Cette expression met en évidence le rôle des covariances croisées entre les variables (c.-à-d., et ), ainsi que des covariances directes entre les variables (c.-à-d., et , dans la précision de l’estimation.
L’optimisation des vecteurs de poids et sous les contraintes de non-biais conduit au système de cokrigeage ordinaire (CO) et au système de cokrigeage simple (CS) lorsque ne tient pas compte des contraintes.
Cokrigeage ordinaire (CO)¶
On cherche à construire une estimation linéaire de la variable principale à partir des observations des variables principale et secondaire ( et ) par l’estimateur suivant :
L’estimateur doit être sans biais, ce qui s’assure par les contraintes suivantes:
Par rapport au krigeage ordinaire, on constate l’ajout d’une contrainte supplémentaire liée à la variable secondaire. Cette contrainte indique que la somme des poids des variables secondaires doit être nulle. Cela tient au fait que l’espérance de l’estimateur doit être égale à la moyenne du processus aléatoire . Ainsi, on doit avoir . Cela est vrai uniquement si et si .
Tout comme dans le krigeage ordinaire, nous allons devoir former un Lagrangien afin de tenir compte de nos deux contraintes de non-biais. On forme le Lagrangien en introduisant deux multiplicateurs de Lagrange, et , et la fonction à minimiser s’écrit alors :
On dérive en fonction des poids et ainsi que des multiplicateurs. Cela donne le système de cokrigeage ordinaire suivant :
La variance d’estimation associée est :
Ce système s’écrit de façon compacte en forme matricielle :
Où désigne la matrice des covariances entre toutes les observations de la variable principale, la matrice des covariances croisées entre les observations de la variable principale et celles de la variable secondaire, et la matrice des covariances entre les observations de la variable secondaire. On note que la matrice de cokrigeage reste symétrique ; on a ainsi que , où est l’opérateur de transposition.
Les vecteurs et représentent, respectivement, les poids associés aux observations de la variable principale et de la variable secondaire, tandis que et sont les vecteurs de covariances entre le point à estimer et les observations de la variable principale et de la variable secondaire, respectivement.
Note : Pour effectuer un cokrigeage ordinaire, il faut disposer d’au moins une observation de la variable principale et deux observations de la variable secondaire. La raison est la suivante : il est nécessaire d’attribuer un poids à au moins une coordonnée associée à la variable principale afin de satisfaire la contrainte de somme des poids égale à 1. De plus, il faut au moins deux observations de la variable secondaire pour satisfaire à la contrainte de somme des poids nulle imposée aux variables secondaires. S’il n’y avait qu’une seule observation secondaire, son poids serait nul pour respecter cette contrainte, et le système se réduirait alors à celui du krigeage ordinaire.
Cokrigeage simple (CS)¶
Si les moyennes des variables et , notées respectivement et , sont connues, il est possible de centrer les données et de travailler directement sur les résidus. Les résidus correspondent à la partie décentrée des variables, c’est-à-dire à la différence entre chaque observation et sa moyenne :
On estime alors le résidu , puis on lui ajoute la moyenne pour obtenir l’estimation finale :
De cette manière, on peut omettre les contraintes de non-biais du cokrigeage ordinaire, à condition de disposer d’une estimation suffisamment précise des moyennes et .
Ainsi, l’estimateur devient :
avec les poids obtenus par résolution du système suivant :
La variance d’estimation est alors :
Le systèmede cokrigeage simple s’écrit de façon compacte en forme matricielle de la manière suivante:
Note : Contrairement au cokrigeage ordinaire, on peut ici réaliser une estimation même sans observations de la variable principale, à condition d’avoir au moins une observation de la variable secondaire. Si aucune observation de la variable secondaire n’est disponible, il ne s’agit plus d’un cokrigeage, mais simplement d’un krigeage.
Cas particulier¶
Si l’une des deux variables possède une moyenne connue, par exemple lorsque la moyenne de la variable principale est inconnue mais celle de la variable secondaire est connue, on peut construire un système d’équations qui satisfaite cette contrainte.
Dans ce cas, seules les observations de la variable principale sont soumises à la contrainte de non-biais. Tandis qu’aucune contrainte n’est imposée aux poids de la variable , car les résidus ont une moyenne nulle. Ainsi, on obtient une seule contrainte :
L’estimateur s’écrit alors :
où seule la moyenne de est soustraite, puisque celle de demeure inconnue.
On forme le Lagrangien en introduisant un seul multiplicateur de Lagrange sur la variable , soit , et la fonction à minimiser s’écrit alors :
On dérive en fonction des poids et , ainsi que du multiplicateur de Lagrange. Cela donne le système de cokrigeage suivant :
où est le multiplicateur de Lagrange associé à la contrainte de non-biais.
La variance d’estimation correspondante est donnée par :
Ce système s’écrit de façon compacte en forme matricielle :
Remarquez qu’il n’y a pas de grande différence entre le système de cokrigeage simple, ordinaire et celui-ci. Il faut simplement adapter les lignes de 1 et de 0, pour tenir compte de la contrainte de biais de manière adéquate selon la connaissance ou non des moyennes des processus aléatoires et .
Remarque :
Ce cas est courant lorsque la variable secondaire provient d’un modèle ou d’une mesure exhaustive déjà centrée, tandis que la variable principale repose sur un échantillonnage partiel.
Changement de paradigme¶
Dans la majorité des applications pratiques du krigeage, on préfère le krigeage ordinaire. Pourquoi ? Parce qu’il permet de relâcher l’hypothèse stricte de stationnarité en supposant une quasi-stationnarité, c’est-à-dire une moyenne qui varie localement (lentement) dans l’espace, avec une structure de covariance constante à l’intérieur du voisinage d’estimation. Cette approche rend le krigeage ordinaire robuste face à des écarts modérés à la stationnarité, car la moyenne est considérée comme localement constante dans chaque voisinage de recherche. À l’inverse, le krigeage simple exige une stationnarité d’ordre deux complète, où la moyenne et la covariance doivent être constantes sur l’ensemble du domaine. Ainsi, nous avons tendance à utiliser le KO. De plus, l’outil de base est le variogramme, car il nous est possible de modéliser des scénarios où l’on ne connaît pas le palier, sans avoir besoin de la moyenne de la variable principale.
En revanche, dans le cas du cokrigeage, la situation est légèrement différente. On utilise le plus souvent le cokrigeage simple, notamment dans les contextes où la variable principale n’est pas observée à certains endroits, mais où des variables secondaires corrélées sont disponibles. Un exemple classique est l’estimation de la densité des roches (souvent non observée) à partir de levés gravimétriques (données échantillonnées de manière très exhaustive). Dans le cokrigeage, la covariance — et non le variogramme — devient l’outil fondamental, puisqu’elle permet de décrire les relations conjointes et potentiellement asymétriques entre les variables principales et secondaires, ce que le variogramme ne permet pas. De plus, la covariance croisée permet de tenir compte de données colocalisé, ce que le variogramme croisée ne permet pas. Nous allons voir cela à la section suivante.