Certaines méthodes de simulation ne permettent pas de générer directement des simulations conditionnelles, c’est-à-dire des réalisations qui respectent exactement les valeurs observées aux points d’échantillonnage. Pour contourner cette limitation, on utilise une technique appelée post-conditionnement par krigeage. Cette approche consiste à ajuster une réalisation non conditionnelle afin qu’elle coïncide parfaitement avec les données observées tout en conservant sa structure spatiale.
Principe du post-conditionnement¶
On suppose que la variable aléatoire est gaussienne de moyenne nulle. La démarche est la suivante :
Simulation non-conditionnelle
On réalise une simulation non-conditionnelle, , sur les points à simuler ainsi que sur les points échantillons.On note les valeurs simulées aux points échantillons (qui ne correspondent pas encore aux observations réelles).
Krigeage des données observées et simulées
On effectue ensuite un krigeage (simple ou ordinaire) aux points à simuler en utilisant deux jeux de données distincts :: les valeurs krigées obtenues à partir des données observées ;
: les valeurs krigées obtenues à partir des valeurs simulées aux points échantillons, . On obtient ainsi deux champs krigés : l’un fondé sur les observations réelles, l’autre sur les valeurs simulées, ce qui permet de mesurer l’erreur à corriger.
Calcul de la simulation conditionnelle post-conditionnée
La simulation conditionnelle corrigée s’obtient en ajustant la simulation non conditionnelle :
Cette relation corrige la simulation non conditionnelle en lui ajoutant l’écart entre le krigeage fondé sur les observations et celui fondé sur les valeurs simulées. Le résultat est alors conditionnel, c’est-à-dire qu’il reproduit exactement les valeurs observées tout en conservant la structure spatiale de la simulation initiale.
La Fig. 1 illustre le principe du post-conditionnement par krigeage. On y observe que pour rendre conditionnelle une simulation initialement non conditionnelle, il suffit de lui additionner l’erreur de krigeage entre les observations et la simulation, ce qui force la réalisation à respecter exactement les valeurs échantillonnées.
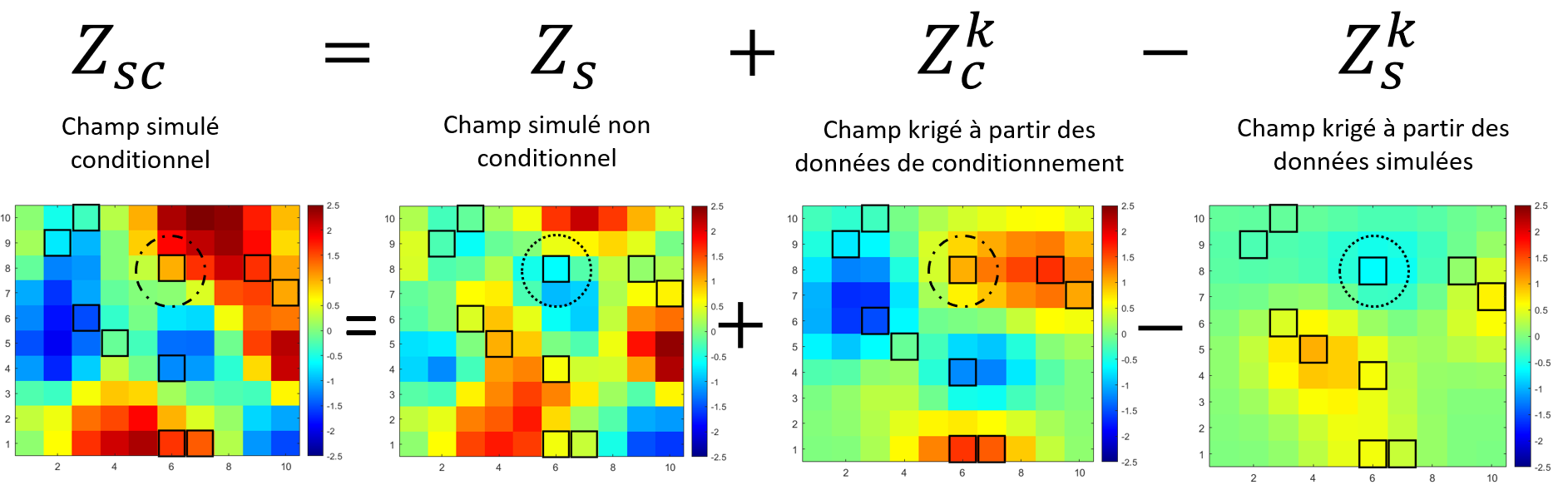
Figure 1:Principe du post-conditionnement par krigeage.
Propriétés¶
Exactitude aux points échantillons :
Si un point à simuler coïncide avec un point échantillon, alors :
La simulation post-conditionnée reproduit parfaitement la valeur observée.
Très loin des points échantillons, on a , donc : la simulation post-conditionnée tend vers la simulation non-conditionnelle.Précision :
On peut démontrer que l’erreur entre la simulation conditionnelle post-conditionnée et la valeur simulée non conditionnelle vérifie :
où est la variance du krigeage simple. Cela signifie qu’une seule simulation conditionnelle issue du post-conditionnement est, en moyenne, deux fois moins précise qu’un estimateur par krigeage simple. Il ne faut donc jamais utiliser une seule réalisation post-conditionnée comme estimateur.Moyenne des simulations conditionnelles :
Si l’on génère un grand nombre de simulations conditionnelles post-conditionnées et que l’on en calcule la moyenne, on retrouve exactement l’estimateur de krigeage simple. La variance d’estimation de cette moyenne correspond alors à la variance du krigeage simple, et la dispersion des différentes réalisations autour de cette moyenne est également égale à cette même variance. Le post-conditionnement permet donc, après moyennage, de reconstituer à la fois l’estimation et l’incertitude du krigeage simple, tout en fournissant des réalisations respectant la variabilité naturelle du phénomène.
La Fig. 2 illustre quelques propriétés des simulations conditionnelles et non conditionnelles, en mettant en évidence leurs différences de comportement et leurs relations avec les observations.

Figure 2:Propriétés des simulations conditionnelles et non conditionnelles.
En résumé¶
Le post-conditionnement est une technique efficace pour adapter des simulations non-conditionnelles afin qu’elles respectent les données observées.
Bien qu’une simulation post-conditionnée unique soit moins précise qu’un krigeage, l’ensemble des réalisations permet d’obtenir une bonne estimation et une mesure fiable de l’incertitude.