Hydrogéologie¶
Domingue (1994, mémoire de maîtrise) a évalué l’efficacité du piège hydraulique de Ville-Mercier pour confiner les contaminants présents dans le roc fracturé. Pour ce faire, il a utilisé les mesures de capacité spécifique (tirées de l’annuaire des puits et forages du Québec) pour estimer les transmissivités. Ces transmissivités ont servi de points conditionnants pour des simulations de champs de transmissivités. Ces champs ont été utilisés, conjointement avec les charges connues et les conditions aux limites, pour simuler le réseau d’écoulement. Domingue a pu ainsi définir la zone de confinement associé au piège hydraulique pour 3 réalisations différentes du champ de transmissivité. Pour au moins une des réalisations, la zone contaminée n’était pas incluse totalement dans la zone de captage. En conséquence, le piège hydraulique pourrait être inefficace.
Gutjahr et al. (1995) ont utilisé les simulations conditionnelles afin de comparer le pouvoir conditionnant des charges et de la transmissivité pour déterminer le trajet d’un contaminant et le temps de déplacement avant d’arriver à la frontière du champ étudié. Il a montré, entre autres, que les charges possédaient un fort pouvoir conditionnant sur le trajet suivi par le contaminant, mais un très faible pouvoir conditionnant sur les temps de parcours (et donc les vitesses). Au contraire, les transmissivités ont un faible pouvoir conditionnant sur les trajets, mais un fort pouvoir sur les temps de parcours. Toutefois, c’est la combinaison des deux informations (charge et transmissivité) qui conditionne le mieux les temps de parcours.
Gomez-Hernandez (1993) a utilisé les simulations conditionnelles pour effectuer les changements d’échelle des transmissivités à partir de la mesure quasi-ponctuelle vers des blocs de taille équivalente à celle utilisée dans la simulation d’écoulement. Il a défini un champ de la taille du bloc souhaitée et a simulé les transmissivités sur des supports comparables à ceux observés. Il a d’abord imposé des frontières imperméables sur les côtés nord et sud des blocs pour déterminer la transmissivité est-ouest, puis sur les côtés est et ouest pour déterminer les transmissivités nord-sud. Il a ensuite déduit les modèles de covariance croisée liant les transmissivités ponctuelles aux transmissivités de blocs (nord-sud et est-ouest) ainsi que les covariances simples et croisées des transmissivités de blocs. Il a utilisé ces modèles de covariance dans une simulation conditionnelle pour produire des champs de transmissivité de blocs à partir de valeurs ponctuelles de transmissivité.
Gomez-Hernandez (1996) a utilisé les simulations conditionnelles comme champs initiaux pour résoudre le problème inverse en hydrogéologie. Il obtient plusieurs champs de transmissivités différents, tous satisfaisant les charges observées. Ces champs pourraient être utilisés pour modéliser le rendement d’un aquifère, l’efficacité d’un piège hydraulique, la sensibilité à la contamination, etc.
Mines¶
Naraghi et Marcotte (1996) ont utilisé les simulations conditionnelles pour déterminer le nombre (et l’épaisseur) de couches à utiliser dans une pile d’homogénéisation afin d’obtenir le degré d’homogénéité désiré.
Marcotte et al. (1996) a utilisé les simulations conditionnelles pour décrire l’impact du biais conditionnel des estimateurs sur les profits d’une mine type. Ils ont étudié l’influence de divers facteurs sur ces profits, en particulier la quantité d’observations disponibles lors de l’estimation finale conduisant à la sélection des blocs.
Froideveaux (1984) a utilisé les simulations conditionnelles pour modéliser la précision des estimations des réserves récupérables (i.e. après application d’une teneur de coupure).
Pétrole¶
Les exemples d’application en pétrole sont les plus nombreux mais aussi les plus complexes. La complexité provient en premier lieu de la complexité géologique des réservoirs (failles, paléochenaux, types de roche, etc.), du peu de données directes (forer un puits coûte extrêmement cher) et de l’abondance des données indirectes (relevés de sismique réflexion, diagraphies, observations de champs pétroliers comparables, données de production (débits, pressions, etc.), expertise géologique, etc. La plupart des études combinent plusieurs méthodes de simulation (méthodes booléennes, points marqués, simulations géostatistiques).
Haas et Dubrule (1994) ont utilisé les simulations conditionnelles séquentielles pour effectuer l’inversion 3D des impédances acoustiques. Leur approche consiste à générer un vecteur d’impédance vertical, à convertir la coordonnée z en coordonnée t, à calculer l’amplitude sismique théorique correspondante et à comparer la trace synthétique ainsi obtenue à la trace mesurée. Si les 2 traces sont assez semblables, le vecteur d’impédance est accepté et on passe à un autre vecteur vertical. Sinon, on resimule au même point un autre vecteur vertical et ainsi de suite.
Autres applications potentielles¶
On pourrait utiliser les simulations conditionnelles pour:
calculer la précision de l’estimation des volumes contaminés au-delà d’une certaine norme.
modéliser la variabilité des teneurs observées au concentrateur et étudier l’impact des modifications du plan de minage sur cette variabilité.
étudier différents scénarios de conception d’une fosse à ciel ouvert et déterminer les emplacements optimaux pour les équipements. On pourrait envisager la même chose pour les exploitations souterraines mais le problème est beaucoup plus complexe.
pour une cimenterie, fournir une base de données de « carrières » possibles sur lesquelles tester l’effet d’homogénéisation de différents procédés (sautage, récupération et chargement, broyage, etc.) en vue d’optimiser les modes d’exploitation.
en environnement, pour l’emmagasinage de déchets nucléaires, fournir des bases de données permettant d’étudier les probabilités d’occurrence de scénarios pessimistes. • en environnement ou en hydrogéologie, identifier les emplacements névralgiques où des échantillons supplémentaires devraient être prélevés.
etc.
Remarque à propos de la normalité des observations¶
Comme mentionné précédemment, les méthodes gaussiennes nécessitent que les données conditionnantes suivant une distribution multinormale. On ne peut jamais être certain que cette hypothèse est réaliste. On peut toutefois s’assurer que la distribution des valeurs soit normale par une transformation appropriée. On peut aussi tester en partie si la distribution est binormale, mais guère plus.
En pratique, il faut donc généralement :
Transformer les données vers une distribution normale (via une transformation graphique ou autre méthode).
Calculer et modéliser le variogramme des valeurs transformées.
Effectuer la simulation dans le domaine transformé (normal).
Appliquer la transformation inverse pour revenir au domaine original.
La Fig. 2 illustre ce principe à l’aide de la méthode de transformation graphique. Les données observées sont d’abord classées par rang, ce qui permet d’associer leur fonction de répartition empirique à celle d’une loi normale de moyenne nulle et de variance unitaire. Chaque valeur est ainsi transformée en son quantile normal correspondant, produisant une variable approximativement gaussienne.
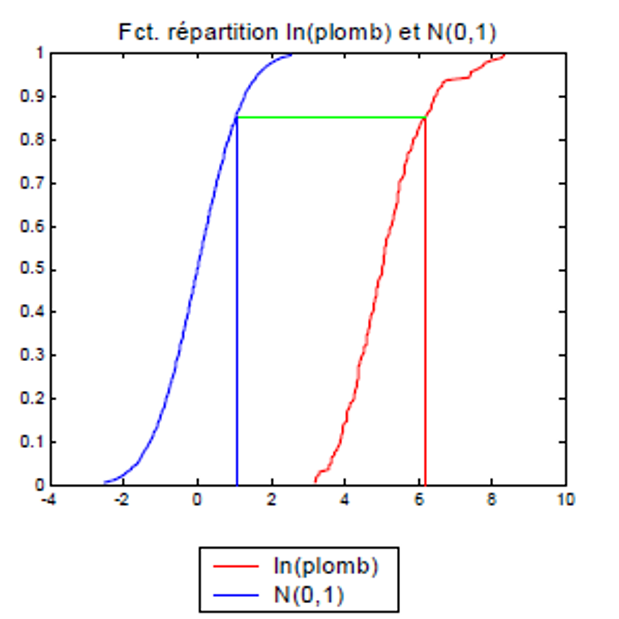
Figure 1:Exemple de transformation graphique des données observées vers la loi normale. À noter qu’ici, les données sont préalablement transformées par le logarithme avant le classement.
On notera que cette procédure assure la reproduction du variogramme de la variable transformée, non celui de la variable originale. La qualité de la reproduction du variogramme original dépendra largement du caractère réaliste, face au comportement des données, des hypothèses de stationnarité et de multinormalité des méthodes de simulation. Toutefois, comme mentionné précédemment, le conditionnement par des données libère en quelque sorte le modèle de ces contraintes, puisque les caractéristiques implicitement contenues dans les données seront préservées et, dans une certaine mesure, propagées aux autres données.
Remarque Il faut aussi garder à l’esprit que l’histogramme et le variogramme ne sont que les deux premiers moments du processus. Il est possible de générer plusieurs processus ayant le même histogramme et le même variogramme, et pourtant présentant une apparence très différente.
Extension au cas multivariable¶
Pour la méthode LU, la simulation multivariable est directe : on travaille avec les matrices de covariance multivariables.
Pour la méthode SGS, il suffit de remplacer le krigeage simple par un cokrigeage simple.
La distribution conditionnelle multivariée est déterminée par les propriétés de la loi multinormale, avec les paramètres obtenus par cokrigeage.