La théorie de Lane et Taylor repose sur le principe de la maximisation du profit net par tonne de matériau minéralisé, ou de la valeur actuelle nette (VAN). Autrement dit, il s’agit de calculer les revenus générés par l’exploitation, puis d’en soustraire les coûts afin d’obtenir le profit net. La dimension temporelle est également prise en compte, puisque le système est dynamique et évolue au fil du temps.
Dans l’approche de Taylor seuls les coûts d’exploitation sont pris en compte. À pleine capacité du concentrateur, les coûts fixes et variables sont inclus dans le calcul des profits. Si le concentrateur est sous-utilisé, seuls les coûts variables sont considérés. Ainsi, la teneur de coupure est constante sauf si l’on actualise les revenus, auquel cas elle décroît dans le temps (Fig. 1).
L’approche de Lane inclut un coût d’opportunité en plus des coûts d’exploitation. Le coût d’opportunité représente le rendement attendu sur la partie non encore exploitée du gisement. Ce coût diminue avec l’avancement de l’exploitation, entraînant une baisse progressive de la teneur de coupure (Fig. 1). À pleine capacité, tous les coûts sont considérés. Sinon, les coûts fixes et d’opportunité peuvent être négligés.
En règle générale, la teneur de coupure obtenue par la méthode de Lane est supérieure ou égale à celle obtenue par la méthode de Taylor, qui néglige les coûts d’opportunité (variables ). Ainsi, Taylor pose . Nous verrons l’impact des coûts d’opportunité dans les exemples interactifs.
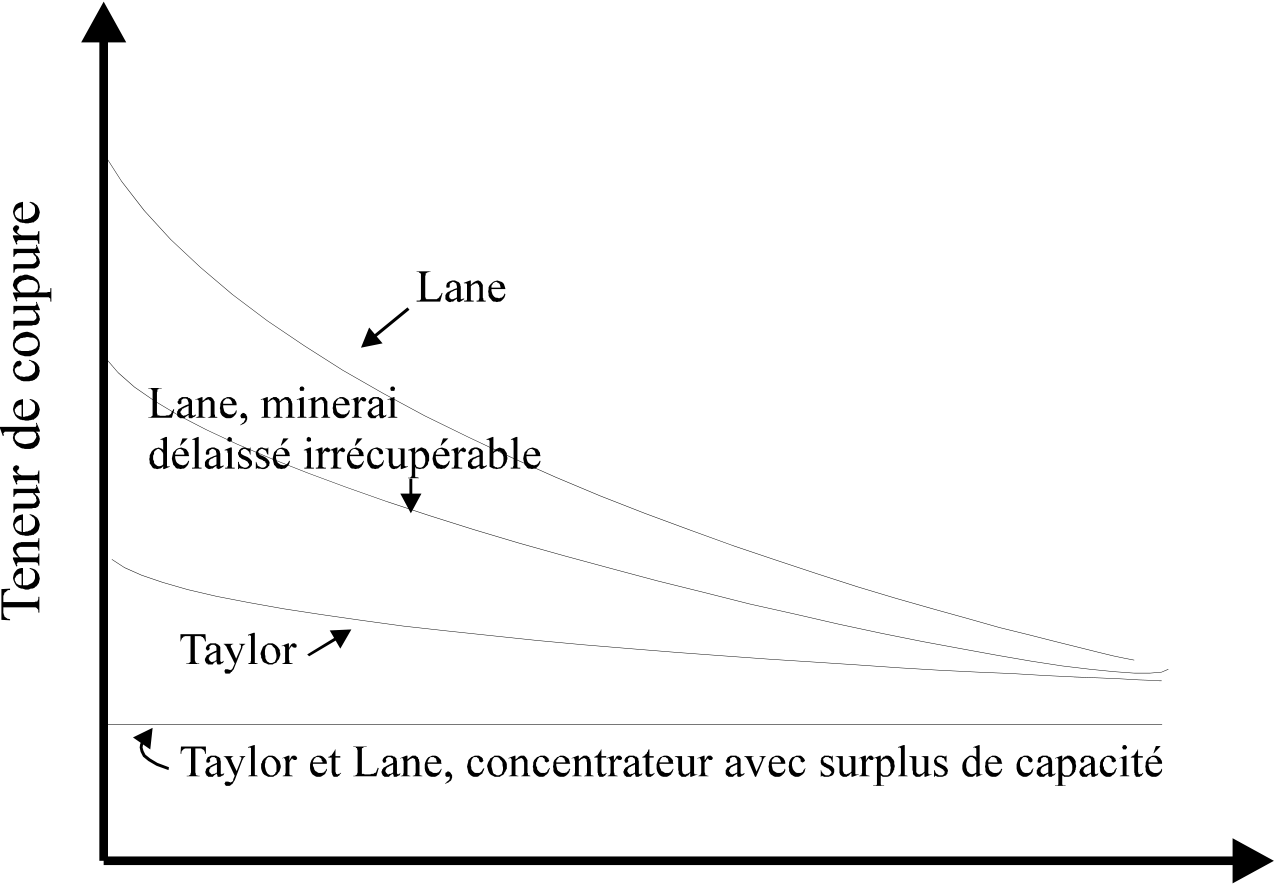
Figure 1:Évolution de la teneur de coupure selon la méthode utilisée.
D’autres facteurs peuvent influencer la teneur de coupure. Une baisse des prix des métaux pousse à augmenter la teneur de coupure[1], car nous allons concentrer nos efforts sur les teneurs riches de notre gisement. Par la suite, il existe le concept de récupération ultérieure, c’est-à-dire que si la mine à la capacité de stocker des minerais légèrement en dessous de la teneur de coupure optimale, il est probable qu’à long terme ces minerais deviennent rentables. Ainsi, nous pourrions laisser sur place une certaine quantité de minerai à être traitée ultérieurement, et ainsi augmenter la teneur de coupure.
Les coûts variables (variable - [coûts variables de minage] et variable - [coûts variables de traitement]) et le coût d’opportunité (variable - [coût d’opportunité]) sont, par définition, variables dans le temps, c’est-à-dire qu’ils sont recalculés en fonction de l’évolution du système minier (agrandissement de la mine, découvertes de nouvelles zones exploitables, dysfonctionnement des équipements, évolution de la demande du marché, ...). Cette dynamique est très technique et requiert une connaissance approfondie du système financier et de l’exploitation minière. Dans le cadre de cette lecture, nous aborderons le calcul de la teneur de coupure pour un instant donné. Ainsi, les variables nécessaires pour réaliser les calculs seront toujours fournies. Aucune analyse financière des marchés ne sera réalisée.
En pratique, le choix de l’approche et des hypothèses influence fortement la stratégie d’exploitation. Ces méthodes supposent une bonne connaissance de la distribution des teneurs, ce qui nécessitera une étude géostatistique rigoureuse (effet de support, information disponible, etc.), abordée dans une prochaine lecture. Pour le reste de cette lecture, nous supposerons que nous sommes toujours en mesure d’obtenir des estimations de nos ressources dans les règles de l’art. Dans le cas contraire, cela sera mentionné et nous étudierons les impacts des mauvaises estimations.
Sauf si une hausse est attendue à court terme. Nous ne changerons pas nos stratégies pour une variation à court terme, sauf si des coûts d’opportunité sont identifiés