Dans la plupart des cas, les décisions doivent être prises sur des supports différents de ceux des données observées. Or, la fonction estimée précédemment est valable uniquement pour le support ponctuel des observations.
Par exemple, dans une mine, la probabilité qu’un bloc de 125 m³ atteigne une teneur de coupure donnée n’est pas la même que celle d’une carotte de 1 m. Comme la variance varie selon le support, les fonctions de répartition associées sont nécessairement différentes. Il est donc indispensable de corriger la fonction afin de tenir compte du changement de support.
Note :
On pourrait penser qu’il suffit de remplacer le krigeage ponctuel du KI par un krigeage par blocs. Cependant, représente l’estimation de la probabilité moyenne que les points du bloc soient inférieurs à , et non la probabilité que la valeur moyenne du bloc soit inférieure à .Cette distinction est importante car la probabilité n’est pas un opérateur linéaire par rapport à la moyenne, tout comme le logarithme n’est pas linéaire par rapport à la moyenne (i.e., ).
Correction affine¶
La correction affine, la plus utilisée avec le KI, repose sur l’hypothèse que la distribution des blocs est identique à celle des points, à une contraction près, donnée par le rapport des écarts-types (ou variances) des blocs et des points.
Formellement, la correction affine s’écrit :
où :
est la moyenne locale (i.e., l’espérance obtenue de la fonction de répartition estimée par KI au point ponctuel),
est la variance (dispersion) au support du bloc,
est la variance au support ponctuel.
Exemple¶
Pour l’exemple précédent de la section 10.3, on peut calculer une espérance conditionnelle de , et un rapport de variances de .
On cherche la probabilité que le bloc dépasse la valeur 9.
Le seuil ponctuel équivalent devient :
En se référant au tableau précédent, la probabilité d’excéder ce seuil au point est :
Tandis que la probabilité ponctuelle d’excéder le seuil 9 est plus élevée :
Limitations et remarques¶
La correction affine ne peut pas être utilisée pour des changements de support trop importants, typiquement lorsque . Dans ce cas, la forme de l’histogramme change trop fortement, et la méthode perd en pertinence. La Fig. 1 illustre l’impact de la correction affine sur la fonction de répartition : la différence entre la courbe noire et la courbe rouge correspond simplement à une contraction d’amplitude, exactement égale au rapport . Ainsi, la correction affine n’est pas adaptée lorsque les blocs considérés sont trop grands par rapport à la structure spatiale du phénomène. Dans ce contexte, on s’attend à une diminution progressive du nombre de modes et à un histogramme local qui tend vers une loi normale. La fonction de répartition des blocs devrait alors refléter cette normalité émergente.
Pour de tels changements de support, il faut recourir à des méthodes plus sophistiquées. Une approche consiste à utiliser des simulations géostatistiques ponctuelles conditionnelles, qui reproduisent le variogramme et respectent les observations. En agrégeant ces simulations à l’échelle des blocs, on peut estimer directement la fonction de répartition locale des blocs. De nombreuses techniques de simulation sont disponibles pour ce type d’analyse.
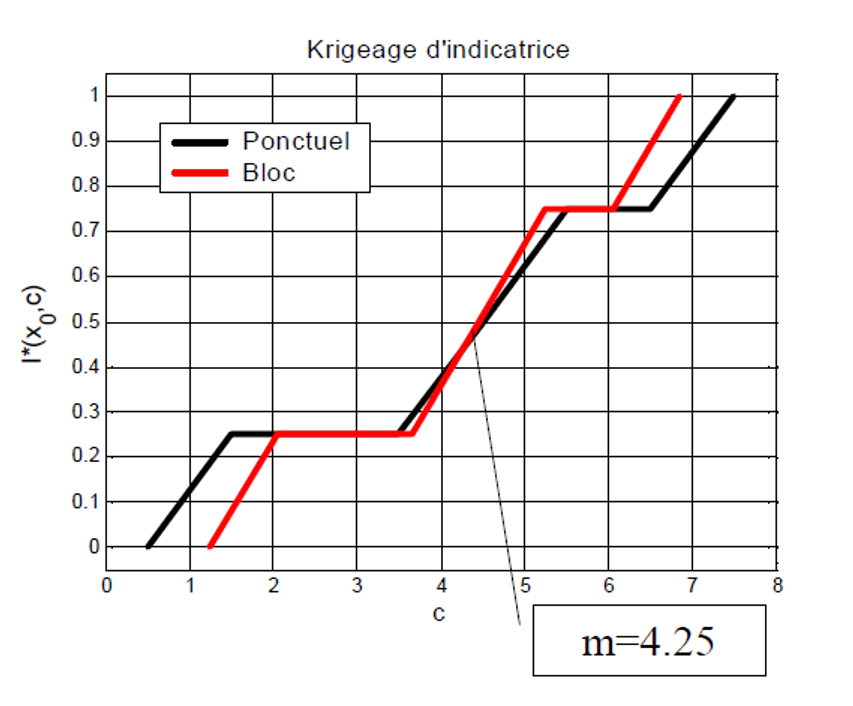
Figure 1:Impact de la correction affine sur la fonction de répartition.
Cette correction affine permet donc une adaptation simple et souvent efficace du KI aux problèmes pratiques où les supports d’estimation et d’observation diffèrent.