Comme mentionné précédemment, rien ne garantit que le résultat du krigeage d’indicatrices sera une fonction respectant les propriétés d’une fonction de répartititon :
si
Il faut donc, avant tout calcul, s’assurer que la fonction estimée respecte ces propriétés, sans quoi des résultats aberrants, comme des probabilités négatives, pourraient apparaître. Pour cela, on effectue des corrections dites “ad hoc”.
La Fig. 1 illustre, de manière exagérée, la violation des propriétés attendues d’une fonction de répartition.
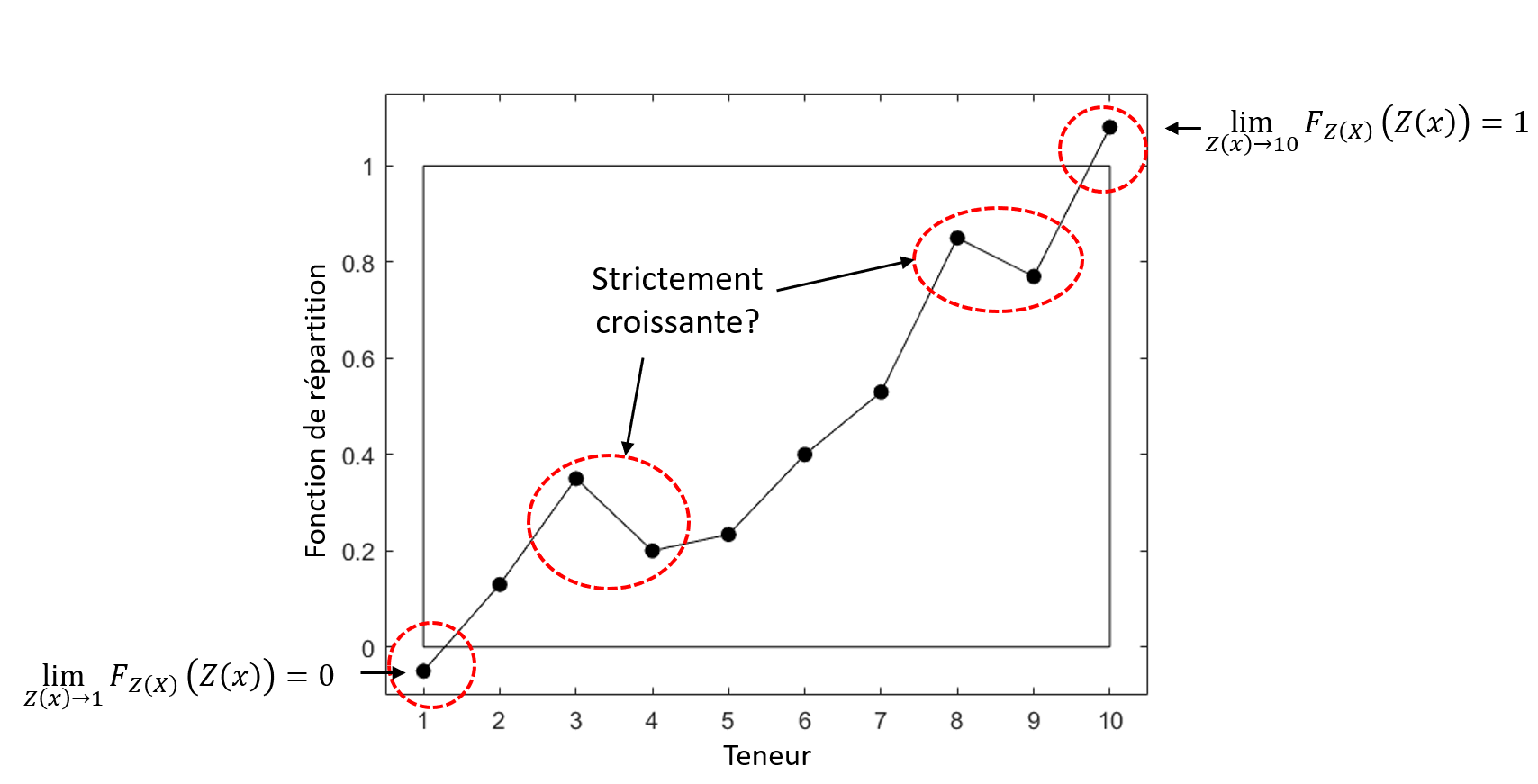
Figure 1:Violation des propriétés d’une fonction de répartition.
Correction « ad hoc » de la fonction de répartition estimée¶
Troncature des bornes :
Mettre les valeurs négatives de égales à 0, et celles supérieures à 1 égales à 1.Correction vers l’avant :
Soient les seuils ordonnés .
On définit la fonction corrigée vers l’avant par :Pour :
Correction vers l’arrière :
On définit la fonction corrigée vers l’arrière par :Pour :
Fonction corrigée finale :
La fonction corrigée est obtenue en faisant la moyenne des deux corrections :
Exemple de correction¶
Le tableau suivant illustre la correction appliquée à une fonction présentant des anomalies :
| Seuil | ||||
|---|---|---|---|---|
| 1 | -0.01 → 0 | 0 | 0 | 0 |
| 2 | 0.13 | 0.13 | 0.13 | 0.13 |
| 3 | 0.24 | 0.24 | 0.234 | 0.237 |
| 4 | 0.238 | 0.24 | 0.234 | 0.237 |
| 5 | 0.234 | 0.24 | 0.234 | 0.237 |
| 6 | 0.237 | 0.24 | 0.237 | 0.2385 |
| 7 | 0.53 | 0.53 | 0.53 | 0.53 |
| 8 | 0.79 | 0.79 | 0.77 | 0.78 |
| 9 | 0.77 | 0.79 | 0.77 | 0.78 |
| 10 | 1.02 → 1.0 | 1.0 | 1.0 | 1.0 |
Exemple visuel¶
La Fig. 2 illustre l’application des corrections des relations d’ordre présentées dans le tableau précédent. On y observe l’effet de la correction avant et de la correction arrière. Visuellement, la correction préalable consiste à remplacer chaque valeur par le maximum entre celle-ci et la valeur précédente, ce qui garantit une fonction strictement croissante. À l’inverse, la correction arrière part du seuil le plus élevé et remplace chaque valeur par le minimum entre celle-ci et la valeur du seuil situé à un rang supérieur, ce qui produit une fonction strictement décroissante. Les deux corrections définissent une enveloppe dont on prend généralement la moyenne pour obtenir une fonction de répartition corrigée et conforme aux relations d’ordre.
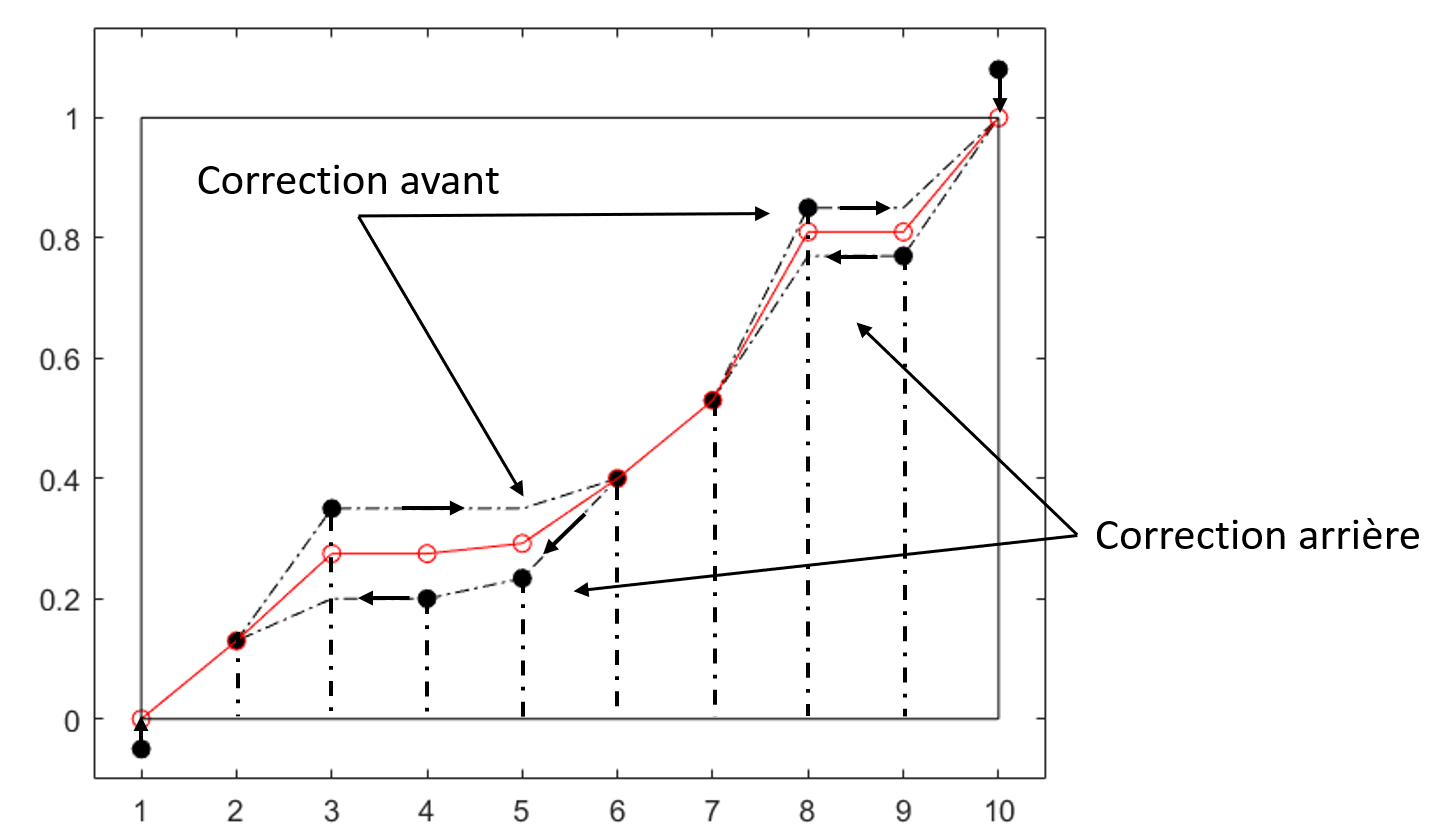
Figure 2:Correction des relations d’ordre de l’exemple du tableau ci-haut.