On considère quatre valeurs observées aux positions , formant un rectangle. On souhaite effectuer un krigeage d’indicatrices (KI) au point , situé au centre de ce rectangle :
On choisit les seuils .
Par symétrie, le krigeage ordinaire fournit les poids :
Pour chaque seuil , les indicatrices sont définies par :
Le krigeage d’indicatrices donne :
La table suivante résume les valeurs obtenues :
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 1/4 |
| 4 | 1 | 0 | 0 | 0 | 1/4 |
| 5 | 1 | 0 | 0 | 1 | 1/2 |
| 6 | 1 | 1 | 0 | 1 | 3/4 |
| 7 | 1 | 1 | 1 | 1 | 1 |
Cette table constitue une approximation discrète de la fonction de répartition conditionnelle :
La Fig. 1 présente le tableau sous forme de graphique. On y observe la fonction de répartition discrète ainsi estimée. À partir de ce graphique, il est ensuite possible de calculer plusieurs grandeurs, comme illustré ci-dessous.
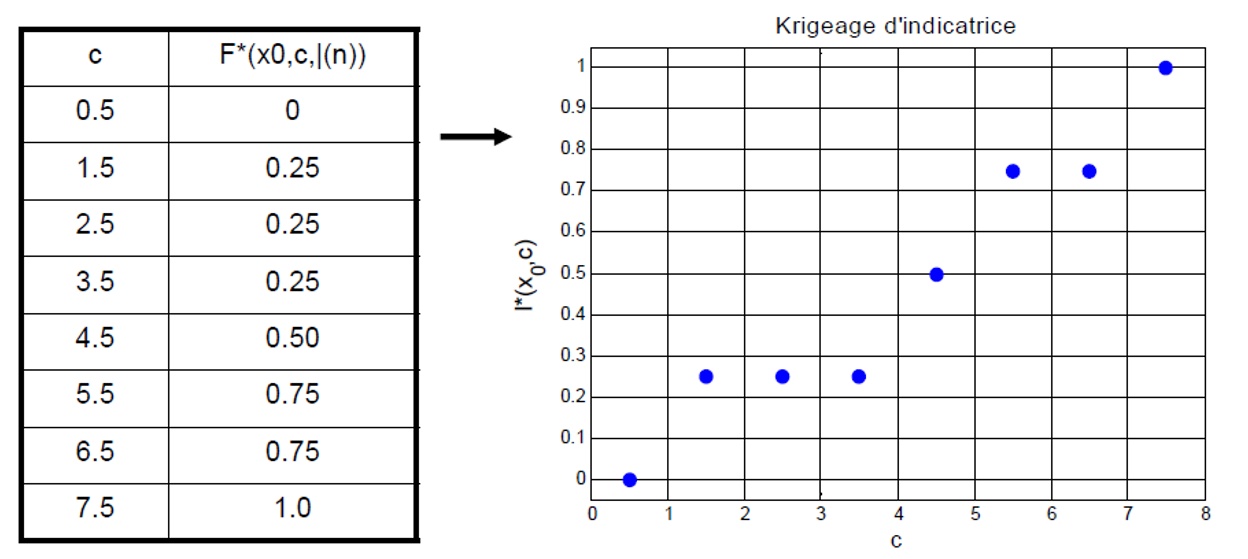
Figure 1:Fonction de répartition estimée au point .
1. Quelle est la probabilité qu’au point la valeur soit supérieure à 3.5, à 4.3?¶
Formule générale :
Pour ¶
Pour ¶
Interpolation linéaire entre 4 et 5 :
Donc :
2. Quelle est la médiane de la distribution au point ? Quelle est la valeur correspondant au 65ᵉ percentile ?¶
La médiane satisfait :
Comme :
Pour le 65e percentile, on cherche tel que :
On constate que cela se produit entre les seuils 5 et 6. Ainsi, on doit faire l’interpolation linéaire pour retrouver le seuil correspondant au 65ᵉ percentile :
.
3. Quelle est l’espérance mathématique de au point ?¶
Le KI fournit une distribution discrète sous la forme d’une probabilité d’appartenance aux classes définies par des seuils. Pour obtenir l’espérance mathématique, on associe à chaque classe une valeur représentative. Celle-ci peut provenir de l’histogramme global (moyenne des observations dans chaque intervalle) ou, plus simplement, être prise comme le milieu de la classe.
L’espérance estimée s’écrit alors :
En utilisant les milieux de classes et les probabilités issues du KI, on obtient l’espérance conditionnelle au point par :
Notes :¶
Cet estimateur est sans biais pour car (et donc ) est sans biais pour . Cela signifie qu’en moyenne, les erreurs d’estimation sont nulles, car la fonction de répartition estimée par KI coïncide avec la fonction de répartition réelle de .
On observe aussi que lL’estimé par krigeage ordinaire au point serait :
Dans la pratique, les probabilités pour la dernière classe ne sont pas toujours nulles. Il est difficile de sélectionner une valeur représentative pour cette classe (semi-ouverte). Un choix arbitraire doit être fait, ce qui peut influencer l’espérance. Une possibilité est d’ajuster la valeur pour que la moyenne des espérances calculées par KI coïncide avec la moyenne des valeurs krigées. Une autre est de prendre la moyenne des données originales dans cette classe.
4. Quelle est la variance conditionnelle de au point ?¶
La variance conditionnelle peut être calculée directement à partir de la fonction de répartition discrète estimée par le KI.
On utilise la formule classique :
Pour cela, il faut d’abord calculer l’espérance du carré :
Les milieux de classes et probabilités non nulles sont :
| Intervalle | ||
|---|---|---|
| [3,4) | 2.5 | 0.25 |
| [4,5) | 4.5 | 0.25 |
| [5,6) | 5.5 | 0.25 |
| [6,7) | 6.5 | 0.25 |
On calcule donc :
L’espérance déjà obtenue est :
Ainsi, la variance conditionnelle estimée est :
5. Quelle est l’espérance associée à un coût ?¶
Supposons que l’on connaisse une fonction de coût associée aux valeurs de (par exemple un coût de décontamination qui augmente en fonction du niveau de contamination). On aimerait connaitre la valeur de ce coût. Supposon que , alors on a :
où est le nombre de seuils considérés, la valeur krigée pour le seuil (avec et ), et une valeur représentative de la classe (centre de la classe ou moyenne de l’histogramme global).
Ici, avec pour et , 0 ailleurs, l’espérance du coût est donc :
Krigeage simple d’indicatrice¶
La formulation simple du krigeage d’indicatrice est la suivante :
où est la proportion globale des données telles que . Les poids sont obtenus en résolvant le système de krigeage simple (KS) basé sur la covariance ou le variogramme des indicatrices pour le seuil considéré.
Le krigeage simple d’indicatrices est particulièrement intéressant lorsque la distribution globale est bien connue ou lorsque l’on dispose d’un grand volume de données fournissant une estimation fiable de . Dans ces situations, la moyenne globale des indicatrices constitue une information précieuse : elle représente la probabilité globale d’être sous le seuil et sert d’ancre probabiliste. Le krigeage simple permet d’intégrer cette information directement dans l’estimation locale, tout en pondérant correctement la contribution des données voisines via les poids issus du variogramme.
En comparaison avec le krigeage ordinaire d’indicatrices, le KSI offre une solution plus stable lorsque les données sont peu nombreuses ou très dispersées, car le terme évite que l’estimation locale dérive en l’absence de support spatial suffisant. Autrement dit, si les données voisines sont rares, éloignées ou peu corrélées, l’estimation locale se rapproche naturellement de la distribution globale, ce qui est cohérent d’un point de vue probabiliste.
Lorsque le variogramme est un effet de pépite pur, les poids sont nuls et l’estimation se réduit à la distribution globale :
Cela signifie que l’espace n’apporte aucune information supplémentaire — seule la probabilité globale a du sens. À l’inverse, si le variogramme montre une forte continuité spatiale, les poids deviennent significatifs (typiquement dans l’exemple ci-haut), et l’estimation locale s’appuie alors davantage sur les données voisines.