Une simulation géostatistique vise à générer une réalisation possible d’une variable régionalisée, représentant un phénomène ou un processus naturel que l’on souhaite modéliser. En pratique, on cherche généralement à ce que la simulation reproduise fidèlement les deux premiers moments du processus — son histogramme et son variogramme — de façon à respecter à la fois la distribution globale et la structure spatiale de la variable. Ces approches occupent une place centrale en géostatistique non linéaire, où elles constituent souvent le seul moyen techniquement viable pour estimer certaines grandeurs.
En effet, les méthodes d’estimation géostatistique classiques, comme le krigeage, fournissent la meilleure estimation linéaire au sens du moindre carré, mais produisent inévitablement des résultats lissés. Elles échouent donc à reproduire la variabilité naturelle du phénomène, pourtant essentielle lorsque le problème étudié implique des comportements non linéaires, des changements d’échelle ou des fonctions de transfert complexes. Les simulations, en préservant explicitement cette variabilité, offrent un cadre adapté pour capturer la richesse des structures spatiales nécessaires à une modélisation plus réaliste.
Une méthode de simulation est dite non conditionnelle lorsqu’elle permet de générer des champs aléatoires qui reproduisent la structure spatiale (variogramme) et l’histogramme inférés à partir des données observées, mais sans chercher à respecter les valeurs effectivement mesurées. Chaque exécution de l’algorithme produit une réalisation possible du phénomène ; en répétant l’algorithme autant de fois que désiré, on obtient un ensemble de réalisations, toutes indépendantes les unes des autres, qui partagent les mêmes caractéristiques statistiques globales soit l’histogramme et le variogramme.
À l’inverse, une méthode de simulation conditionnelle poursuit les mêmes objectifs — reproduire l’histogramme et le variogramme — mais impose en plus que toute réalisation soit compatible avec les données observées. Autrement dit, aux emplacements où des échantillons existent, la valeur simulée doit être exactement égale à la valeur mesurée. Les réalisations reproduisent donc non seulement la variabilité spatiale souhaitée, mais aussi l’information ponctuelle disponible, ce qui les rend directement utilisables pour des analyses locales ou des prédictions physique.
Exemples de simulations en 1D¶
La Fig. 1 illustre un ensemble de réalisations non conditionnelles (en haut) et conditionnelles (en bas). On constate que, dans le cas conditionnel, les courbes bleues — correspondant aux différentes réalisations — passent exactement par les points observés, représentés par les cercles rouges. À l’inverse, les réalisations non conditionnelles ne tiennent pas compte de ces observations et ne les reproduisent donc pas.
L’élément le plus important à remarquer est l’absence de l’effet de lissage typique du krigeage : chacune des courbes bleues présente une variabilité comparable à celle de la courbe noire représentant la réalisation « réelle » ou le processus sous-jacent. C’est précisément l’objectif principal des simulations géostatistiques : reproduire la variabilité naturelle de la variable régionalisée, tout en respectant la structure spatiale et, dans le cas conditionnel, les observations disponibles.
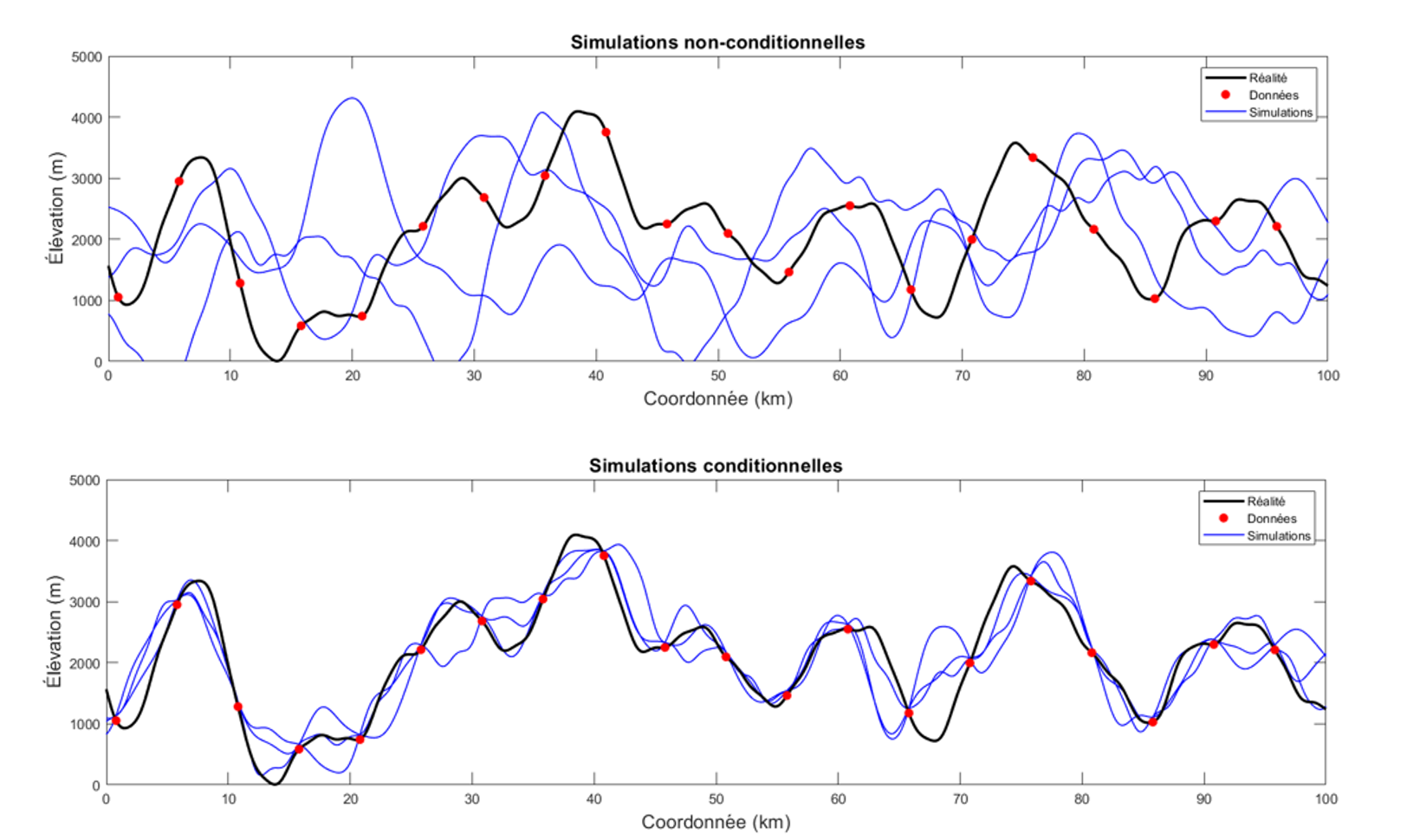
Figure 1:Simulations non conditionnelles versus simulations conditionnelles
Ainsi, l’objectif d’une simulation géostatistique est de reproduire, en moyenne, le variogramme théorique imposé. Chaque réalisation possède son propre variogramme, légèrement différent d’une simulation à l’autre en raison du caractère aléatoire du processus. Toutefois, lorsque l’on considère la moyenne des variogrammes calculés sur un grand nombre de réalisations, celle-ci converge vers le variogramme du modèle théorique. La Fig. 2 illustre ce principe : les variogrammes expérimentaux obtenus à partir de 100 réalisations (lignes grises) présentent une certaine variabilité, mais leur moyenne (étoiles noires) s’aligne presque parfaitement sur le modèle théorique (ligne rouge).
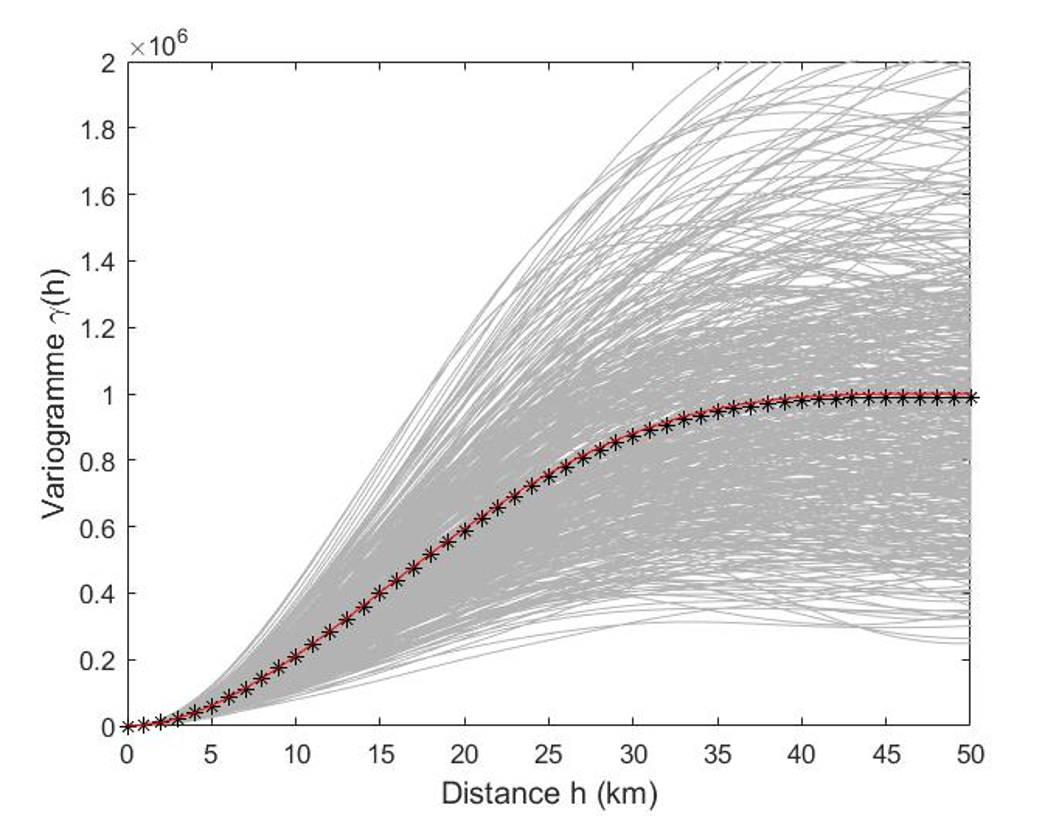
Figure 2:Variogrammes expérimentaux de 100 réalisations (lignes grises), leur moyenne (étoiles noires) et comparaison au modèle théorique (ligne rouge).
Information complémentaire¶
Dans la pratique, les simulations conditionnelles sont généralement privilégiées lorsqu’il s’agit de résoudre des problèmes concrets, car elles intègrent l’information déjà disponible et garantissent que les réalisations reproduisent fidèlement les données observées. Les simulations non conditionnelles, quant à elles, sont surtout utilisées pour tester des méthodes, des modèles ou des algorithmes, puisqu’elles ne sont contraintes par aucune observation.
Les méthodes de simulation visent principalement à reproduire les statistiques d’ordre 1 (moyenne) et d’ordre 2 (variance-covariance), c’est-à-dire l’histogramme et le variogramme du phénomène. Les statistiques d’ordre supérieures ne peuvent généralement pas être spécifiées et dépendent de la méthode de simulation choisie et, dans le cas des simulations conditionnelles, des données conditionnantes. Une exception notable est la méthode du recuit simulé, qui permet d’intégrer explicitement certaines statistiques d’ordre supérieur au processus de génération. Par ailleurs, des travaux récents portent sur la modélisation directe des asymétries spatiales, qui constituent précisément une statistique d’ordre supérieur et constituent un nouvel axe de recherche prometteur en géostatistique moderne.
Il est important de souligner que les données conditionnantes influencent fortement les caractéristiques statistiques des réalisations, y compris pour les deux premiers ordres. Il est, par exemple, impossible de simuler un variogramme incompatible avec la structure spatiale révélée par ces données. Par ailleurs, les observations confèrent une certaine robustesse aux résultats : différentes méthodes de simulation tendent à produire des réalisations comparables lorsqu’elles sont conditionnées aux mêmes données.
Enfin, le présent chapitre se concentre uniquement sur la simulation d’une variable continue dans un domaine donné. Dans d’autres contextes, il peut être nécessaire de simuler d’abord des objets géologiques tels que des chenaux, des lentilles ou des structures stratigraphiques, avant d’y appliquer des propriétés quantitatives. Il est également possible de s’intéresser à la simulation de variables discrètes, telles que les lithologies, mais ces aspects dépassent le cadre de la discussion présentée ici.