Référence : P.M. Gy, 1992. Sampling of heterogeneous and dynamic material systems, theories of heterogeneity, sampling and homogenizing. Elsevier, Amsterdam, 653 p.
P. Gy est un ingénieur des mines qui s’est penché sur le problème de l’échantillonnage en adoptant un point de vue statistique. Il a développé une formule permettant de prédire la précision relative d’un échantillon pour représenter la teneur d’un lot donné, en fonction de la taille des fragments, de la masse de l’échantillon et du lot, ainsi que de différents paramètres minéralogiques et granulométriques.
Cette formule est toutefois valide à la condition que l’échantillon soit un échantillon probabiliste.
Échantillon probabiliste
Un échantillon probabiliste, pour un lot donné, est un échantillon dans lequel chaque fragment du lot possède une probabilité non nulle d’être sélectionné. L’échantillon est considéré comme sans biais lorsque tous les fragments ont une probabilité égale d’être sélectionnés.
La Fig. 1 présente une illustration comparant un échantillonnage déterministe (Fig. 1A) à un échantillonnage probabiliste (Fig. 1B). Pour qu’un échantillonnage soit considéré comme probabiliste, chaque particule de la carotte doit avoir une chance égale d’être sélectionnée pour l’analyse finale. Ainsi, sélectionner uniquement une zone spécifique de la carotte (échantillonnage déterministe) ne permet pas de bien représenter l’ensemble de celle-ci.
Comment peut-on être assuré que la section prélevée représente fidèlement la teneur réelle de la carotte ? Il se peut que l’on soit extrêmement chanceux et que l’on prélève l’unique section de la carotte contenant de l’or, ce qui biaiserait fortement l’estimation de sa teneur globale. Il est donc essentiel d’assurer une représentation probabiliste de la carotte, comme illustré en bas de la Fig. 1B.
À noter que, généralement, une demi-carotte est envoyée pour analyse, tandis que l’autre moitié est entreposée dans une carothèque. Cela permet un suivi rigoureux et la réalisation d’études complémentaires (géologiques, minéralogiques, géomécaniques, etc.).
Plusieurs compagnies explorent aujourd’hui la possibilité de numériser les carottes (photographies haute résolution, imagerie géophysique) afin de se départir des échantillons physiques. L’idée est que l’intelligence artificielle pourrait, à terme, extraire toute l’information pertinente à partir de ces données numériques.
Si cette approche présente des avantages indéniables — notamment la libération d’espace — elle soulève également des questions. À mon avis, rien ne remplace encore l’observation directe d’une carotte à la loupe par un œil humain entraîné. Reste à voir où cette évolution technologique nous mènera dans le futur !

Figure 1:Exemple d’un échantillon déterministe et d’un échantillon probabiliste.
Équation de Gy¶
Soit un certain lot de minerai, par exemple, une demi-carotte de forage de longueur de 3m. Supposons que l’on concasse cette carotte jusqu’à ce que la taille des plus gros fragments soit (en cm). On définit comme la taille du tamis qui retient uniquement les 5 % des fragments les plus gros, c’est-à-dire ceux qui représentent 5 % du poids total du lot.
Si l’on prélève un échantillon de masse (habituellement faible en rapport avec la masse du lot qu’il représente), alors la variance relative (sans unité) de l’erreur d’échantillonnage, , peut s’écrire comme suit :
où est la masse de l’échantillon, en grammes. est la masse du lot échantillonné, généralement beaucoup plus grande que , aussi en grammes. est le facteur de libération, sans unité. est une constante dont les unités sont des . est la concentration du constituant d’intérêt (exprimée en fraction)
L’approximation est valable seulement lorsque .
Détermination du facteur de libération ¶
La valeur du facteur de libération est donnée par :
où représente la taille à laquelle le constituant d’intérêt est entièrement libéré de la gangue. Il s’agit de la taille, par exemple, que l’or disséminé dans la pyrite devient natif. L’or est alors entièrement libéré de la pyrite. Remarque, le facteur est sans unité.
Détermination de la constante ¶
La constante regroupe plusieurs facteurs et peut s’écrire comme :
avec un facteur de forme, défini comme le rapport du volume d’un fragment sur celui du plus petit cube le contenant entièrement. est sans dimension. un facteur de distribution, décrivant l’uniformité de la taille des fragments et donc relié à la courbe granulométrique. est sans unité. est un paramètre combinant les effets de la teneur et des masses spécifiques du minéral. possède les unités d’une masse spécifique ().
Détermination du facteur de forme¶
Le facteur de forme représente le rapport entre le volume d’un fragment et celui du plus petit cube pouvant entièrement le contenir. Par exemple, pour un fragment de forme sphérique de diamètre 1 cm, le plus petit cube pouvant contenir cette sphère est un cube dont les côtés mesurent 1 cm. Le volume de la sphère est alors , alors que le volume du cube est de 1 , ce qui donne .
Pour un minéral fibreux (comme l’amiante) ou tabulaire (par exemple le mica), le facteur de forme est beaucoup plus faible, généralement compris entre et .
Après de nombreuses analyses en laboratoire sur divers minéraux, une valeur recommandée pour la plupart des minerais est . Il convient toutefois de noter que ce n’est pas une règle universelle, et qu’il est préférable de consulter la littérature pour identifier le facteur approprié au matériau étudié.
Par souci de simplicité, nous utiliserons ici systématiquement la valeur :
Détermination du facteur de distribution¶
Le facteur de distribution décrit l’uniformité de la courbe granulométrique. Il peut être estimé à partir des diamètres caractéristiques de la distribution, soit et , selon la règle suivante :
Cependant, la calibration précise des courbes granulométriques est relativement rare dans les laboratoires miniers en raison du temps et des coûts que cela implique. Il est important de rappeler qu’une compagnie minière peut avoir à faire analyser plusieurs milliers de carottes. Disposons-nous réellement du temps et des ressources nécessaires pour établir une courbe granulométrique détaillée pour chaque échantillon dans le but d’estimer précisément le facteur ? En règle générale, la réponse est non.
D’ailleurs, l’utilisation du dans la formule de Gy n’est pas anodine. De nombreuses analyses expérimentales ont été menées en laboratoire pour établir une corrélation entre la distribution granulométrique et le facteur de distribution (Fig. 2). Il a été observé que, pour un grand nombre d’échantillons, la valeur du facteur tend à se rapprocher de 0.25 lorsqu’on utilise dans les calculs. Ainsi, pour des raisons de simplicité et d’efficacité, nous adopterons systématiquement, dans nos calculs, la valeur :
Détermination du facteur ¶
Le facteur est un paramètre combinant les effets de la teneur et des masses spécifiques. Il est défini comme :
où :
est la masse spécifique du constituant d’intérêt (en ),
est la masse spécifique de la gangue (en ),
est la concentration du constituant d’intérêt (exprimée en fraction : 10 % = 0.10, 10 ppm = 0.00001).
Remarque 1. La gangue est constituée de toute la matière qui n'est
pas le constituant d'intérêt.Remarque 2. Le constituant d'intérêt est souvent le minéral qui
contient le métal recherché. Par exemple : Pour le cuivre : la
chalcopyrite (CuFeS2), Pour le zinc : la sphalérite (ZnS), Pour l'or : la pyrite
(FeS2), ou parfois l'or natif.Exemple : Soit une analyse indiquant une teneur de 5 % en cuivre (Cu). Le cuivre provient de la chalcopyrite, de formule CuFeS2. La valeur de doit donc représenter la fraction massique de chalcopyrite, et non celle de cuivre. Il faut donc convertir la teneur en cuivre en teneur équivalente en chalcopyrite, en utilisant les masses molaires.
La masse molaire de la chalcopyrite est donnée par :
Le rapport massique du cuivre dans la chalcopyrite est donc :
Ainsi, une teneur de 5 % en cuivre correspond à une teneur de :
Cette valeur est utilisée pour le calcul du facteur .
À noter que cette relation est vraie si le cuivre est uniquement présent dans la chalcopyrite.
Interprétation de la formule de Gy¶
La formule précédente est valide uniquement pour un échantillon probabiliste, c’est-à-dire qu’au sein du lot échantillonné, chaque fragment doit avoir une probabilité égale d’être sélectionné. Toute déviation par rapport à ce modèle augmente la variance relative d’estimation, et peut même introduire des biais significatifs.
Si, après un broyage à la taille , on prélève une masse pour analyse, on commet une erreur d’échantillonnage dont l’importance, relativement à la teneur, est influencée par plusieurs facteurs :
elle augmente lorsque les fragments sont isométriques (facteur ) ;
elle augmente avec l’homogénéité de la distribution des tailles des fragments (facteur ) ;
elle augmente avec la taille de libération du constituant d’intérêt (facteur ) ;
elle diminue avec la concentration du constituant d’intérêt (facteur ).
Toutes ces remarques peuvent être tirées de l’analyse de l’équation \ref{eq:gy}.
Au finale, plus la variance de l’erreur est grande, moins l’échantillon est représentatif du lot qu’il est censé représenter.
Cette formule est applicable dans le cas où tout le métal est contenu dans un seul minéral (le constituant d’intérêt). Elle exprime que la précision obtenue (en termes de variance) est proportionnelle à la masse de l’échantillon et inversement proportionnelle au cube de la taille des fragments les plus gros --- ou à lorsque la taille des fragments est supérieure à la taille de libération. En effet, dans ce dernier cas, , et donc la variance relative .
Facteur pris en compte dans la théorie¶
La formule de Gy a été élaborée originalement, pour l’essentiel, à partir de la loi de distribution discrète hypergéométrique qui décrit la probabilité de tirer "x" boules blanches parmi "n" quand le lot en contient boules blanches parmi boules (tirage sans remise). Cela revient à dire , dans notre contexte, la probabilité de tiré élément de la carotte représentative de la teneur de celle-ci parmi élément de la carotte.
Cette loi hypergéométrique, quand est grand, peut être approchée par une loi binomiale. Ainsi, la moyenne et la variance de (concentration mesurée) sont alors (concentration réelle) et , respectivement. La variance relative sera .
Cette formule indique que la concentration du lot () et le nombre de fragments dans l’échantillon () jouent chacun un rôle primordial dans la variance d’échantillonnage. Ainsi, plus la concentration est élevée, plus la variance relative diminue. De même, plus le nombre de fragments dans l’échantillon augmente, plus la variance diminue.
Or, le nombre de fragments est directement proportionnel à la masse de l’échantillon, inversement proportionnel au cube du diamètre, et il est aussi relié à la forme et la densité des fragments (pour une même masse d’échantillon, plus la densité est élevée, moins il y aura de fragments). Tous ces éléments se retrouvent dans la formule de Gy. Il a aussi réussi à incorporer dans sa formule l’influence du fait que les fragments peuvent être composés de gangue et du minéral d’intérêt (facteur de libération ) et le fait que les fragments ne sont pas tous de la même grosseur (facteur granulométrique ).
Examinons ces facteurs à tour de rôle :
Masse de l’échantillon : Plus la masse de l’échantillon augmente, plus il y a de fragments et moins la variance d’échantillonnage est grande (loi binomiale).
Masse du lot : Plus la masse du lot à échantillonner est faible et s’approche de celle de l’échantillon, plus la variance relative d’échantillonnage diminue. À la limite, si l’échantillon représente 100% du lot, il n’y a pas d’erreur d’échantillonnage.
Diamètre des fragments : Plus les fragments sont gros, moins il y en a dans l’échantillon et plus la variance relative augmente.
Forme des fragments (facteur « ») : Pour une même distribution granulométrique, des fragments plats ou allongés montreront un volume plus faible. À densité égale, une masse donnée d’échantillon comprendra donc plus de fragments s’ils sont plats ou allongés que s’ils sont sphérique.
Taille des fragments homogène vs hétérogène (facteur « ») : Les calculs de la formule de Gy sont faits en considérant les plus gros fragments. Si la courbe granulométrique est très étalée, il y aura plus de fragments au total que si elle est très resserrée.
Taille de libération du minéral d’intérêt (facteur « ») : Si le minéral d’intérêt est entièrement libéré, l’hétérogénéité entre chaque grain est maximale (minéral d’intérêt ou gangue). S’il n’est pas entièrement libéré, les grains sont plus homogènes entre eux et donc un même échantillon devrait être plus précis. À la limite, si chaque fragment avait une concentration exactement égale, il n’y aurait pas de variance d’échantillonnage. Donc la libération maximale est un facteur défavorable toutes autres choses étant égales.
Concentration du constituant d’intérêt (facteur ) : À densité constante, si la concentration du minéral d’intérêt augmente (), il y a plus de fragments du minéral d’intérêt et l’écart relatif entre la vraie proportion et la proportion dans l’échantillon tend à diminuer (voir loi binomiale). De plus, pour une même concentration, si la densité de la gangue et du minéral d’intérêt augmentent alors il y aura moins de fragments. De même, si seule la densité du minéral d’intérêt () augmente, ceci implique une moins grande proportion volumique de fragments du minéral d’intérêt et donc une plus grande variance relative d’échantillonnage (loi binomiale).
Exemples d’application¶
Exemple 1 - Mine de Murdochville¶
La mine de Murdochville fait sauter chaque semaine un volume d’environ . Le minerai est contenu dans la chalcopyrite, dont la masse spécifique est de , tandis que celle de la roche encaissante, la gangue, est de . Les plus gros blocs résultant du sautage ont un diamètre d’environ . On déverse le minerai dans un concasseur qui réduit la taille des blocs à environ . La taille de libération de la chalcopyrite est d’environ . La teneur du volume sauté devrait se situer entre Cu et Cu.
Problème : Quelle masse d’échantillon la mine devrait-elle prélever pour connaître, avec une précision relative de (i.e. ), la teneur en cuivre du volume sauté, dans les deux cas suivants :
échantillonnage directement au chargeur, avant le concassage ;
échantillonnage après le concassage, sur le convoyeur menant au concentrateur.
Solution¶
a) Échantillonnage avant le concassage¶
On pose :
La teneur en chalcopyrite est estimée entre :
En substituant dans l’expression du facteur , on trouve :
On impose une précision relative . En remplaçant dans la formule de variance :
b) Échantillonnage après le concassage¶
Seuls et changent :
On constate donc qu’il est beaucoup plus économique d’échantillonner sur le convoyeur que d’échantillonner aux points de soutirage de la mine. De plus, lors de l’échantillonnage au soutirage, les fragments les plus gros ne peuvent être retenus, introduisant ainsi un biais dans la méthode, qui affecte à la fois la teneur estimée et la variance d’échantillonnage. L’échantillonnage aux points de soutirage présente également un risque opérationnel puisqu’il peut interférer avec la production minière.
Exemple 2 - Gisement d’or disséminé¶
Dans un gisement d’or, où l’or est disséminé et se trouve emprisonné dans la structure de la pyrite (densité de la pyrite : 5 ; densité des roches volcaniques : 3), on prélève des carottes de 1 mètre que l’on divise en 2 demi-carottes. On broie ensuite la demi-carotte en fragments de 2.5 mm et on prélève environ 100 g pour analyse. La procédure est-elle adéquate si la demi-carotte a une teneur de 5 ppm, une taille de libération (de la pyrite), , de 0.1 mm, un facteur de forme, , de 0.5 et un facteur de distribution, , de 0.75 ? La concentration moyenne de l’or dans la pyrite est d’environ 50 ppm.
Supposons que si la carotte renferme 5 ppm d’or, elle renferme 10% de pyrite. On calcule :
On a aussi que :
En utilisant la formule de la précision relative () :
Ce qui donne :
La procédure est excellente, elle permettra une précision de l’ordre de 2%.
Exemple 3 - Gisement d’or natif¶
Dans un contexte similaire à l’exemple 2, si l’or se présente sous forme native (i.e. des pépites d’or), avec une taille de libération de 0.01 mm, la procédure est-elle toujours adéquate ? Ici, le facteur est approximativement :
Le calcul de est réaliser avec , soit 5 ppm. Le constituant d’intérêt est l’or natif cette fois-ci et non la pyrite.
Le facteur de libération est de 0.063 (). Nous posons le facteur de forme égale à 0.2, car l’or se présente sous forme de paillettes, et le facteur de distribution est maintenue à 0.75.
En utilisant la formule de la précision relative :
Ce qui donne :
La procédure est inadéquate. La teneur obtenue à l’analyse se situera entre 0 ppm et 50 ppm dans 95% des cas, alors que la vraie teneur est 5 ppm. Pour avoir une précision acceptable, il faudrait analyser toute la demi-carotte ou broyer beaucoup plus finement que 2.5 mm avant de prélever 100 g pour former l’échantillon. Nous verrons graphiquement comment poser ces diagnostics.
Procédures multistages¶
Les procédures d’échantillonnage nécessitent presque toujours plusieurs étapes successives de broyage et d’échantillonnage. Par exemple, une demi-carotte peut être broyée à 2.5 mm, puis un sous-échantillon de 100 g est prélevé. Ce dernier est ensuite broyé à 0.5 mm, suivi d’un prélèvement de 30 g, qui est à son tour broyé à 0.1 mm, avant de prélever un dernier sous-échantillon de 5 g destiné à l’analyse.
On reconnaît ainsi trois étapes de broyage (2.5 mm, 0.5 mm et 0.1 mm) et trois étapes de sous-échantillonnage (100 g, 30 g, 5 g). Chaque étape de sous-échantillonnage introduit une erreur d’échantillonnage, dont on peut calculer la variance relative à l’aide des équations précédemment présentées. Ces sous-échantillonnages étant réalisés de manière indépendante, les erreurs associées sont également indépendantes. Par conséquent, les variances relatives s’additionnent. Il n’est pas anodin que la phrase précédente soit mise en gras. En statistique, ce sont les variances qui s’additionnent, et non les écarts-types. Or, la formule de Gy fournit un écart-type relatif. Il ne faut donc pas oublier de convertir les écarts-types en variances avant de les additionner.
Dans une procédure d’échantillonnage, c’est donc le maillon faible --- c’est-à-dire l’étape de sous-échantillonnage générant la plus grande erreur --- qui sera responsable de la majorité de la variance totale de l’erreur. Il est essentiel d’identifier ce maillon faible afin d’apporter les ajustements nécessaires et améliorer la représentativité de l’échantillon.
Sur un graphique où l’on porte en abscisse (x) la taille des plus gros fragments (), et en ordonnée (y) la masse de l’échantillon (), on peut représenter chaque étape de concassage ou broyage par un segment horizontal, et chaque étape de sous-échantillonnage par un segment vertical. Il est possible de superposer à ce graphique les courbes de variance relative correspondant à chaque taille et chaque masse d’échantillon (voir section suivante). Cela permet de détecter aisément les étapes critiques qui nécessitent des améliorations pour obtenir un échantillon plus représentatif.
Représentation graphique¶
Les facteurs ayant le plus d’influence sur la variance d’échantillonnage sont nettement la taille des plus gros fragments () et la masse de l’échantillon (). Sur des échelles log-log, la variance d’échantillonnage varie de façon linéaire en fonction de la taille des fragments et de la masse de l’échantillon.
On peut ainsi construire une série de droites sur ce graphique, ayant une pente de 3 lorsque , et une pente de 2.5 lorsque , ces droites représentant des configurations assurant une variance d’échantillonnage constante à chaque étape d’un sous-échantillonnage.
La Fig. 3 présente des isocontours (i.e., des plages de valeur pour et qui fournisseent la même écart-type relative pour les paramètres suivants : .
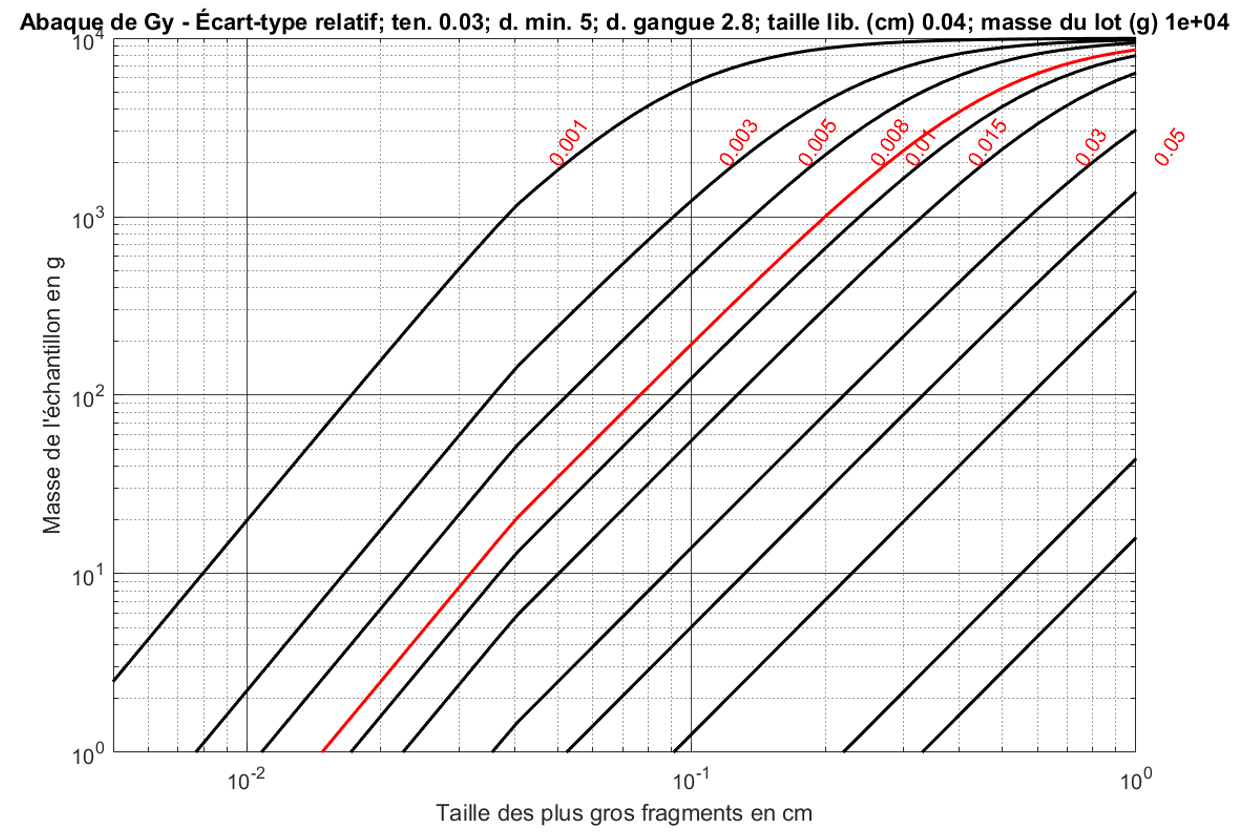
Figure 3:Exemple d’un abaque de Gy pour une procédure multistage.
À partir de cette représentation graphique, il est facile, lorsqu’on connaît la procédure d’échantillonnage en plusieurs étapes (multistage), de la représenter et d’observer visuellement, sans calcul, si la procédure est adéquate.
Par exemple, considérons l’analyse d’une carotte de 10 000 g (). Trois étapes successives de concassage et de broyage sont réalisées pour réduire la taille des fragments à cm, puis à cm, et finalement à cm. À chaque étape, une fraction du lot est prélevée : 5300 g lors de la première étape, 100 g à la deuxième, et enfin 25 g sont prélevés pour l’analyse finale.
La Fig. 4 illustre cette procédure. On part du point A avec une carotte de 10 000 g broyée à une taille de 0,5 cm. On prélève alors 5300 g, ce qui nous amène verticalement au point B. Ce lot est ensuite broyé à une taille de 0,02 cm, nous plaçant au point C. À partir de là, 100 g sont échantillonnés, ce qui nous mène au point D. Ces 100 g sont alors broyés à une taille de 0,007 cm (point E), puis un échantillon final de 25 g est prélevé pour l’analyse (point F).
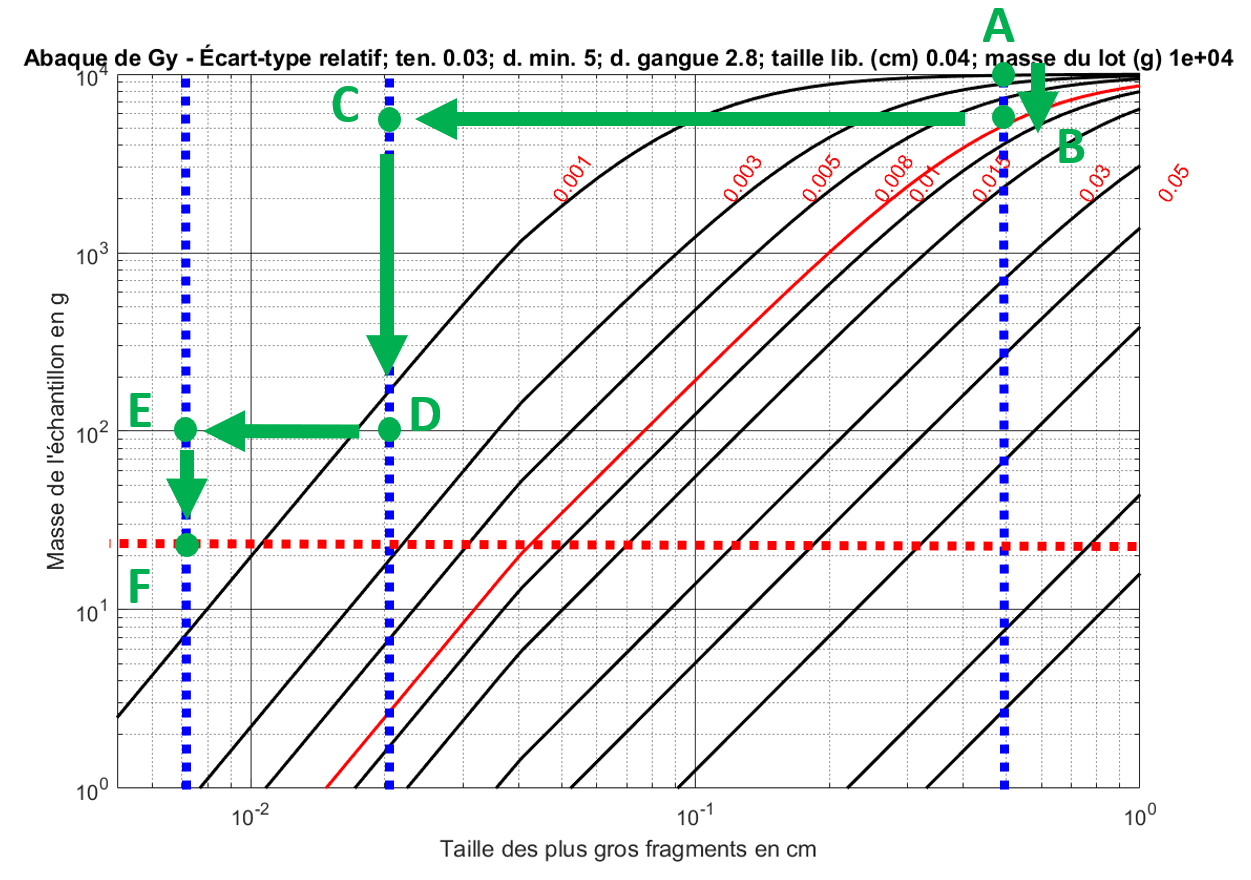
Figure 4:Exemple d’application de l’abaque de Gy pour une procédure multistage.
On note que trois étapes d’échantillonnage sont effectuées. Ce sont uniquement ces étapes d’échantillonnage qui génèrent une erreur d’échantillonnage. Nous supposons qu’aucune perte de matériau n’a lieu lors des étapes de concassage ou de broyage. Ainsi, la variance relative totale peut être obtenue en additionnant les variances relatives associées à chacune des trois étapes d’échantillonnage :
Exemple : Supposons que l’on souhaite une écart-type relative inférieure à 0,008 (ligne rouge sur la Fig. 4). Pour vérifier rapidement si la procédure est adéquate, sans effectuer le calcul complet, il suffit de s’assurer que les points B, D et F (correspondant aux étapes d’échantillonnage) se situent tous au-dessus de la courbe rouge, et qu’au plus un seul point s’en approche. C’est le cas dans cet exemple, ce qui permet de valider la procédure.
Calcul de l’erreur d’échantillonnage global () de l’exemple¶
Données :
Calcul de :
Calcul de :
Calcul des pour chaque étape d’échantillonnage. Noter que la masse du lot (), la masse d’échantillon (), la taille () et la facteur de libération () varie en fonction de l’étape d’échantillonnage.
Étape B
g, g, cmÉtape D
g, g, cmÉtape F
g, g, cm
Erreur globale :
Le calcul complet montre clairement que l’échantillonnage à l’étape B est celui qui introduit le plus de variance. L’erreur relative finale, , est pratiquement égale à celle de l’étape B, . À noter que, dans cet exemple, les valeurs apparaissent égales en raison des arrondis, ce qui n’est pas le cas en réalité.