Krigeage Ordinaire
# Atelier interactif : Krigeage Ordinaire 2D
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
import ipywidgets as widgets
from IPython.display import display
# -----------------------------
# 1. Génération de données synthétiques 2D
# -----------------------------
np.random.seed(0)
# Grille d'estimation
xv, yv = np.meshgrid(np.linspace(0, 100, 50), np.linspace(0, 100, 50))
x_grid = xv.ravel()
y_grid = yv.ravel()
# Points d'échantillonnage (10 points aléatoires)
n_samples = 10
x_samples = np.random.uniform(0, 100, n_samples)
y_samples = np.random.uniform(0, 100, n_samples)
# Valeurs simulées selon une fonction (avec bruit)
z_samples = np.sin(x_samples * 0.05) + np.cos(y_samples * 0.05) + np.random.normal(0, 0.1, n_samples)
# -----------------------------
# 2. Variogramme exponentiel
# -----------------------------
def exponential_cov(h, range_, sill):
return sill * np.exp(-h / range_)
# -----------------------------
# 3. Krigeage Ordinaire 2D avec voisinage fixe
# -----------------------------
def ordinary_kriging_2d(x_grid, y_grid, x_samples, y_samples, z_samples, range_, sill, n_neighbors=6):
est = np.zeros_like(x_grid)
var = np.zeros_like(x_grid)
for i in range(len(x_grid)):
x0, y0 = x_grid[i], y_grid[i]
dists = np.sqrt((x_samples - x0)**2 + (y_samples - y0)**2)
idx = np.argsort(dists)[:n_neighbors]
X_neigh = np.vstack((x_samples[idx], y_samples[idx])).T
Z_neigh = z_samples[idx]
d_matrix = cdist(X_neigh, X_neigh)
d_vector = np.sqrt((X_neigh[:,0] - x0)**2 + (X_neigh[:,1] - y0)**2)
C = exponential_cov(d_matrix, range_, sill)
c0 = exponential_cov(d_vector, range_, sill)
# Ajouter contrainte Lagrange (somme des poids = 1)
C_ext = np.ones((n_neighbors+1, n_neighbors+1))
C_ext[:n_neighbors, :n_neighbors] = C
C_ext[-1, -1] = 0
c0_ext = np.ones(n_neighbors+1)
c0_ext[:n_neighbors] = c0
try:
weights = np.linalg.solve(C_ext, c0_ext)
est[i] = np.sum(weights[:n_neighbors] * Z_neigh)
var[i] = sill - np.dot(weights[:n_neighbors], c0)
except np.linalg.LinAlgError:
est[i] = np.nan
var[i] = np.nan
return est, var
# -----------------------------
# 4. Widgets interactifs
# -----------------------------
range_slider = widgets.FloatSlider(value=20, min=1, max=50, step=1, description='Portée')
sill_slider = widgets.FloatSlider(value=1.0, min=0.1, max=2.0, step=0.1, description='Sill')
def update_kriging_2d(range_, sill):
est, var = ordinary_kriging_2d(x_grid, y_grid, x_samples, y_samples, z_samples, range_, sill)
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
im0 = ax[0].tricontourf(x_grid, y_grid, est, levels=20, cmap='viridis')
ax[0].scatter(x_samples, y_samples, c='r', edgecolor='k', label='Données')
ax[0].set_title('Estimation par Krigeage Ordinaire')
fig.colorbar(im0, ax=ax[0])
im1 = ax[1].tricontourf(x_grid, y_grid, var, levels=20, cmap='magma')
ax[1].scatter(x_samples, y_samples, c='r', edgecolor='k')
ax[1].set_title('Variance du Krigeage')
fig.colorbar(im1, ax=ax[1])
for a in ax:
a.set_xlim(0, 100)
a.set_ylim(0, 100)
a.set_aspect('equal')
a.grid(True)
plt.tight_layout()
plt.show()
widgets.interact(update_kriging_2d, range_=range_slider, sill=sill_slider);
Loading...
Voissinage local
# Atelier interactif : Voisinage local 2D avec anisotropie et quadrants
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
from matplotlib.patches import Ellipse
np.random.seed(42)
# -----------------------------
# 1. Données aléatoires 2D
# -----------------------------
n_points = 50
x_data = np.random.uniform(0, 100, n_points)
y_data = np.random.uniform(0, 100, n_points)
# Point cible à estimer
x0, y0 = 50, 50
# -----------------------------
# 2. Fonction pour déterminer les voisins
# -----------------------------
def find_neighbors(x_data, y_data, x0, y0, azimut, anis_ratio, radius, max_per_quad):
coords = np.vstack((x_data, y_data)).T
center = np.array([x0, y0])
# Translation
shifted = coords - center
# Rotation pour aligner l'ellipse sur l'axe x
theta = -np.radians(azimut)
rot_matrix = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
rotated = shifted @ rot_matrix.T
# Appliquer anisotropie (ellipse : x / a, y / b)
scaled = rotated / np.array([radius, radius / anis_ratio])
distances = np.linalg.norm(scaled, axis=1)
# Sélection initiale dans l'ellipse
in_ellipse = distances <= 1.0
selected_idx = np.where(in_ellipse)[0]
# Application des contraintes par quadrant
final_idx = []
quadrant_counts = [0, 0, 0, 0] # Q1 à Q4
for idx in selected_idx:
dx = x_data[idx] - x0
dy = y_data[idx] - y0
if dx >= 0 and dy >= 0:
q = 0 # Q1
elif dx < 0 and dy >= 0:
q = 1 # Q2
elif dx < 0 and dy < 0:
q = 2 # Q3
else:
q = 3 # Q4
if quadrant_counts[q] < max_per_quad:
final_idx.append(idx)
quadrant_counts[q] += 1
return final_idx
# -----------------------------
# 3. Fonction de visualisation
# -----------------------------
def plot_neighbors(azimut, anis_ratio, radius, max_per_quad):
fig, ax = plt.subplots(figsize=(6,6))
ax.scatter(x_data, y_data, label='Tous les points', color='gray')
ax.scatter(x0, y0, color='red', label='Point cible')
idx_sel = find_neighbors(x_data, y_data, x0, y0, azimut, anis_ratio, radius, max_per_quad)
ax.scatter(x_data[idx_sel], y_data[idx_sel], color='blue', label='Voisins retenus')
# Dessin de l’ellipse anisotrope
ellipse = Ellipse((x0, y0), width=2*radius, height=2*radius/anis_ratio,
angle=azimut, edgecolor='green', facecolor='none', linestyle='--', linewidth=2)
ax.add_patch(ellipse)
ax.set_xlim(0, 100)
ax.set_ylim(0, 100)
ax.set_title("Voisinage local avec ellipse anisotrope et quadrants")
ax.set_aspect('equal')
ax.grid(True)
ax.legend()
plt.show()
# -----------------------------
# 4. Widgets interactifs
# -----------------------------
azimuth_slider = widgets.IntSlider(value=0, min=0, max=180, step=5, description="Azimut (°)")
anis_slider = widgets.FloatSlider(value=2.0, min=0.5, max=5.0, step=0.1, description="Rapport a/b")
radius_slider = widgets.FloatSlider(value=30, min=5, max=80, step=1, description="Rayon")
quad_slider = widgets.IntSlider(value=2, min=0, max=5, step=1, description="Max/Quadrant")
widgets.interact(plot_neighbors, azimut=azimuth_slider, anis_ratio=anis_slider,
radius=radius_slider, max_per_quad=quad_slider);
Loading...
Effet de pépite
# Atelier 4 : Effet de la épépite (nugget effect) sur le krigeage simple vs ordinaire en 2D
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
import ipywidgets as widgets
from matplotlib.colors import Normalize
np.random.seed(0)
# -----------------------------
# 1. Génération de données synthétiques 2D
# -----------------------------
xv, yv = np.meshgrid(np.linspace(0, 100, 50), np.linspace(0, 100, 50))
x_grid = xv.ravel()
y_grid = yv.ravel()
n_samples = 12
x_samples = np.random.uniform(0, 100, n_samples)
y_samples = np.random.uniform(0, 100, n_samples)
z_samples = np.sin(x_samples * 0.05) + np.cos(y_samples * 0.05) + np.random.normal(0, 0.1, n_samples)
# -----------------------------
# 2. Variogramme exponentiel avec effet de épépite
# -----------------------------
def exponential_cov(h, range_, sill, nugget):
return nugget * (h == 0) + (sill - nugget) * np.exp(-h / range_)
# -----------------------------
# 3. Krigeage simple et ordinaire 2D avec voisinage fixe
# -----------------------------
def kriging_2d(x_grid, y_grid, x_samples, y_samples, z_samples, range_, sill, nugget, kind="simple", mean_global=0.0, n_neighbors=6):
est = np.zeros_like(x_grid)
for i in range(len(x_grid)):
x0, y0 = x_grid[i], y_grid[i]
dists = np.sqrt((x_samples - x0)**2 + (y_samples - y0)**2)
idx = np.argsort(dists)[:n_neighbors]
X_neigh = np.vstack((x_samples[idx], y_samples[idx])).T
Z_neigh = z_samples[idx]
d_matrix = cdist(X_neigh, X_neigh)
d_vector = np.sqrt((X_neigh[:,0] - x0)**2 + (X_neigh[:,1] - y0)**2)
C = exponential_cov(d_matrix, range_, sill, nugget)
c0 = exponential_cov(d_vector, range_, sill, nugget)
if kind == "simple":
try:
weights = np.linalg.solve(C, c0)
est[i] = mean_global + weights @ (Z_neigh - mean_global)
except np.linalg.LinAlgError:
est[i] = np.nan
elif kind == "ordinary":
C_ext = np.ones((n_neighbors+1, n_neighbors+1))
C_ext[:n_neighbors, :n_neighbors] = C
C_ext[-1, -1] = 0
c0_ext = np.ones(n_neighbors+1)
c0_ext[:n_neighbors] = c0
try:
weights = np.linalg.solve(C_ext, c0_ext)
est[i] = np.sum(weights[:n_neighbors] * Z_neigh)
except np.linalg.LinAlgError:
est[i] = np.nan
return est
# -----------------------------
# 4. Interface interactive
# -----------------------------
range_slider = widgets.FloatSlider(value=20, min=5, max=50, step=1, description='Portée')
sill_slider = widgets.FloatSlider(value=1.0, min=0.2, max=2.0, step=0.1, description='Sill')
nugget_slider = widgets.FloatSlider(value=0.0, min=0.0, max=1.0, step=0.05, description='Épépite')
def update_kriging(range_, sill, nugget):
est_simple = kriging_2d(x_grid, y_grid, x_samples, y_samples, z_samples,
range_, sill, nugget, kind="simple", mean_global=np.mean(z_samples))
est_ordinary = kriging_2d(x_grid, y_grid, x_samples, y_samples, z_samples,
range_, sill, nugget, kind="ordinary")
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
norm = Normalize(vmin=min(np.min(est_simple), np.min(est_ordinary)), vmax=max(np.max(est_simple), np.max(est_ordinary)))
im0 = ax[0].tricontourf(x_grid, y_grid, est_ordinary, levels=20, cmap='viridis', norm=norm)
ax[0].scatter(x_samples, y_samples, color='red', edgecolor='k')
ax[0].set_title("Krigeage Ordinaire")
fig.colorbar(im0, ax=ax[0])
im1 = ax[1].tricontourf(x_grid, y_grid, est_simple, levels=20, cmap='viridis', norm=norm)
ax[1].scatter(x_samples, y_samples, color='red', edgecolor='k')
ax[1].set_title("Krigeage Simple")
fig.colorbar(im1, ax=ax[1])
for a in ax:
a.set_xlim(0, 100)
a.set_ylim(0, 100)
a.set_aspect('equal')
a.grid(True)
plt.tight_layout()
plt.show()
widgets.interact(update_kriging, range_=range_slider, sill=sill_slider, nugget=nugget_slider);
Loading...
Visualisation 1DD krigeage
# Atelier : Comparaison de 5 modèles de variogramme en 1D pour KS et KO
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
np.random.seed(0)
# -----------------------------
# 1. Données 1D synthétiques
# -----------------------------
x_samples = np.linspace(0, 10, 10)
z_samples = np.sin(x_samples) + np.random.normal(0, 0.1, len(x_samples))
x_grid = np.linspace(0, 10, 100)
# -----------------------------
# 2. Modèles de variogramme
# -----------------------------
def variogram_model(h, model="exp", range_=2.0, sill=1.0, nugget=0.0):
h = np.abs(h)
if model == "exp":
return nugget + (sill - nugget) * (1 - np.exp(-h / range_))
elif model == "gauss":
return nugget + (sill - nugget) * (1 - np.exp(-(h / range_)**2))
elif model == "sph":
return np.where(h <= range_, nugget + (sill - nugget)*(1.5*h/range_ - 0.5*(h/range_)**3), sill)
else:
return np.full_like(h, np.nan)
# -----------------------------
# 3. Krigeage simple et ordinaire en 1D
# -----------------------------
def krige_1d(x_grid, x_samples, z_samples, model, kind="simple"):
n = len(x_samples)
m = len(x_grid)
Z_krig = np.zeros(m)
Var_krig = np.zeros(m)
d_matrix = np.abs(x_samples[:, None] - x_samples[None, :])
C = 1 - variogram_model(d_matrix, model)
for i, x0 in enumerate(x_grid):
d = np.abs(x_samples - x0)
c0 = 1 - variogram_model(d, model)
if kind == "simple":
try:
w = np.linalg.solve(C, c0)
Z_krig[i] = np.mean(z_samples) + w @ (z_samples - np.mean(z_samples))
Var_krig[i] = 1 - w @ c0
except:
Z_krig[i] = np.nan
Var_krig[i] = np.nan
elif kind == "ordinary":
C_ext = np.ones((n+1, n+1))
C_ext[:n, :n] = C
C_ext[-1, -1] = 0
c0_ext = np.ones(n+1)
c0_ext[:n] = c0
try:
w_ext = np.linalg.solve(C_ext, c0_ext)
Z_krig[i] = w_ext[:n] @ z_samples
Var_krig[i] = 1 - w_ext[:n] @ c0
except:
Z_krig[i] = np.nan
Var_krig[i] = np.nan
return Z_krig, Var_krig
# -----------------------------
# 4. Affichage : 5 variogrammes x (KS + KO)
# -----------------------------
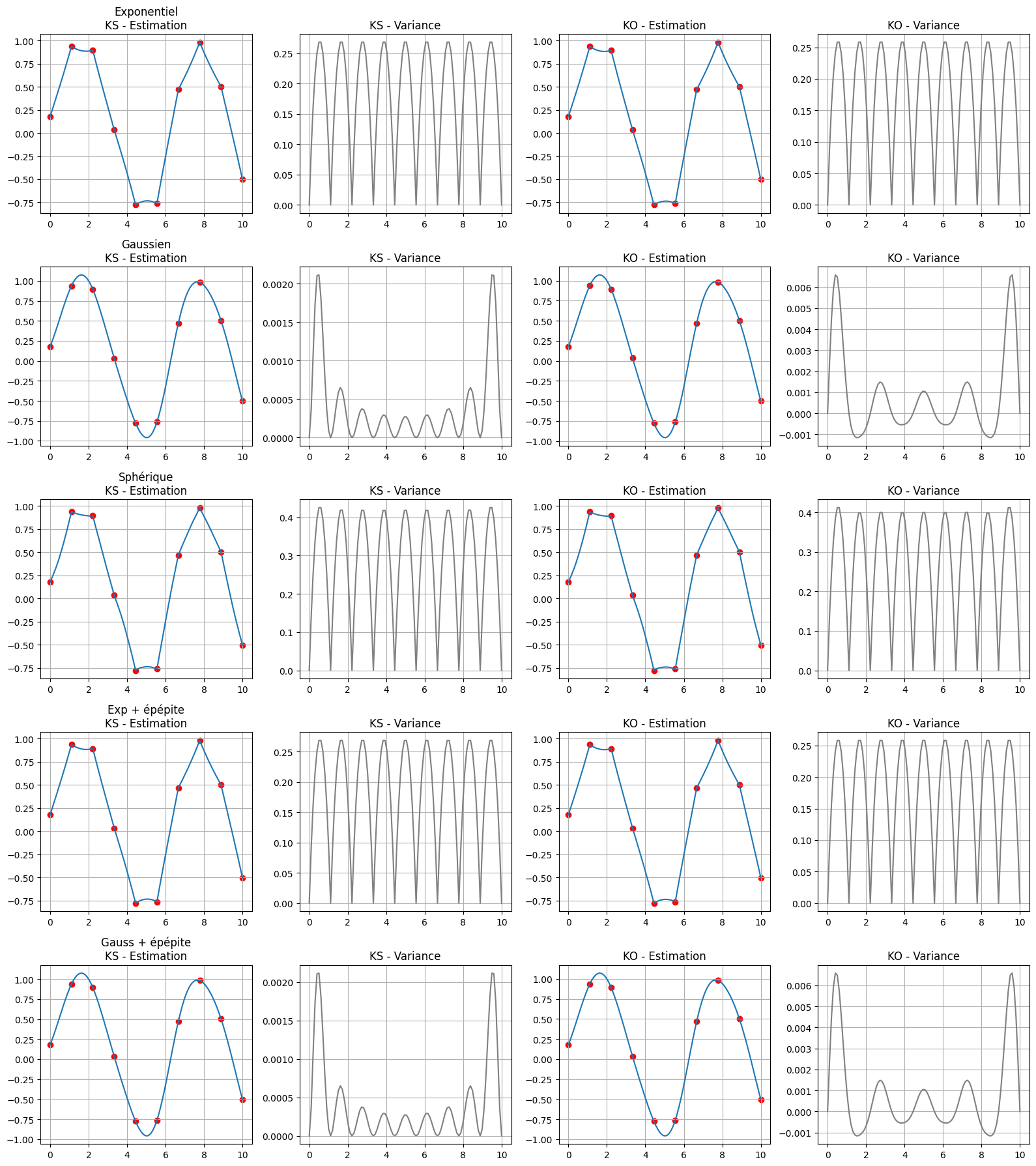
models = ["exp", "gauss", "sph", "exp_nug", "gauss_nug"]
labels = ["Exponentiel", "Gaussien", "Sphérique", "Exp + épépite", "Gauss + épépite"]
fig, axes = plt.subplots(5, 4, figsize=(16, 18))
for i, model in enumerate(models):
model_base = model.replace("_nug", "")
nugget = 0.3 if "nug" in model else 0.0
label = labels[i]
z_ks, var_ks = krige_1d(x_grid, x_samples, z_samples, model_base, kind="simple")
z_ko, var_ko = krige_1d(x_grid, x_samples, z_samples, model_base, kind="ordinary")
axes[i, 0].plot(x_grid, z_ks, label="KS")
axes[i, 0].scatter(x_samples, z_samples, color='red')
axes[i, 0].set_title(f"{label}\nKS - Estimation")
axes[i, 1].plot(x_grid, var_ks, label="Var KS", color='gray')
axes[i, 1].set_title("KS - Variance")
axes[i, 2].plot(x_grid, z_ko, label="KO")
axes[i, 2].scatter(x_samples, z_samples, color='red')
axes[i, 2].set_title("KO - Estimation")
axes[i, 3].plot(x_grid, var_ko, label="Var KO", color='gray')
axes[i, 3].set_title("KO - Variance")
for ax in axes.ravel():
ax.grid(True)
plt.tight_layout()
plt.show()