Comme vu précédemment, il faut non seulement modéliser la structure spatiale d’une variable donnée (p. ex., ), mais aussi la façon dont deux variables distinctes varient ensemble dans l’espace (p. ex., ). Nous savons déjà comment modéliser la structure d’une variable donnée. Ce qui nous manque, c’est un estimateur de cette structure spatiale croisée entre deux variables distinctes.
Il existe deux statistiques expérimentales qui nous permettent d’estimer cette structure spatiale croisée, à savoir la covariance croisée et le variogramme croisé : ces deux fonctions décrivent la dépendance spatiale conjointe entre une variable principale et une variable secondaire .
À noter qu’il existe également le pseudo-variogramme croisé, que nous n’aborderons pas dans cette lecture. Cette mesure permet de combiner les avantages de la covariance croisée et du variogramme croisé ; cependant, elle comporte des inconvénients importants et une complexité d’application accrue. Celui-ci n’est que rarement utilisé.
Covariance croisée¶
Définition¶
La covariance croisée entre deux variables régionalisées et est définie par :
où :
est le vecteur de décalage (lag) partant de la variable vers la variable ,
et sont les moyennes (supposées constantes ou localement constantes).
Cette fonction mesure dans quelle mesure les variations de sont corrélées à celles de à une distance donnée .
Si , les deux variables tendent à augmenter ou diminuer ensemble.
Si , elles varient de manière inverse (corrélation négative).
Si , elles sont indépendantes à cette distance.
Propriétés¶
En général, , mais sous l’hypothèse de stationnarité d’ordre deux, on a :
Cela signifie que la covariance croisée permet de quantifier des asymétries de corrélations.
La valeur à l’origine correspond à la covariance globale entre et , et peut être normalisée pour obtenir le coefficient de corrélation :
Variogramme croisé¶
Définition¶
Le variogramme croisé est défini par :
Relation avec la covariance croisée¶
Sous l’hypothèse de stationnarité d’ordre deux :
Cette relation est directement analogue à celle du cas univarié, où .
Remarques pratiques¶
Il est important de noter que le variogramme croisé est toujours symétrique. C’est-à-dire que nous avons toujours . Ainsi, la covariance croisée ne peut être déduite du variogramme croisé que si celle-ci est symétrique ! En règle générale, la covariance croisée est plus générale que le variogramme croisé, car elle permet d’obtenir des relations non symétriques en fonction de .
Une autre observation importante concerne les paires de points nécessaires au calcul de la covariance croisée, par rapport à celles nécessaires au calcul du variogramme croisé. Pour la covariance croisée, tous les points où l’une ou l’autre des variables est connue peuvent être utilisés pour en calculer la valeur. C’est-à-dire que dès qu’une paire de points existe, elle sera prise en compte dans le calcul de la covariance croisée expérimentale.
Inversement, le variogramme croisé est plus limitatif. Il requiert qu’à une coordonnée , la variable principale et la variable secondaire soient mesurées. Il faut donc quatre observations pour calculer un variogramme croisé, soit les couples et . Ainsi, les données doivent être strictement colocalisées. Toutes les données non colocalisées seront ignorées lors du calcul du variogramme croisé.
Il est important de garder en tête qu’une covariance croisée ou un variogramme croisé négatif à certaines distances est tout à fait normal : cela traduit simplement une corrélation négative entre les deux variables étudiées.
Calcul expérimental de la covariance croisée et du variogramme croisé¶
Définition et formulation¶
Pour deux variables régionalisées et , mesurées aux positions , on cherche à estimer expérimentalement la structure spatiale conjointe.
Covariance croisée expérimentale¶
La covariance croisée expérimentale pour une distance moyenne est donnée par :
où :
est l’ensemble des paires dont la distance appartient à la classe de distance autour de ,
et sont les moyennes des deux variables.
Variogramme croisé expérimental¶
De manière analogue, le variogramme croisé expérimental est défini par :
Exemple numérique¶
La Fig. 1 présente les valeurs de , indiquées à gauche en bleu, et celles de , indiquées à droite en rouge. Nous allons évaluer la covariance croisée expérimentale et le variogramme croisé expérimental à une distance .
Supposons que la moyenne de est et que la moyenne de est . Dans le cas de la covariance croisée expérimentale, il est possible d’identifier 6 couples de points respectant la distance et pour lesquels nous avons une observation de la variable ainsi qu’une observation de la variable secondaire à une distance , soit en . Ces couples () sont les suivants : (6, 3.1) ; (5.9, 5.7) ; (7, 3.1) ; (6.3, 4.7) ; (6.5, 3.3) ; (6.8, 5.3). On obtient ainsi le calcul suivant pour la covariance croisée expérimentale :
Dans le cas du variogramme croisé expérimental, il est possible d’identifier une seule paire de points, respectant la distance, pour laquelle nous avons une observation simultanée des 2 variables aux 2 points de localisation de la variable. Ce couple (,) est le suivant : (6, 5.9, 2.6, 3.1). On obtient ainsi le calcul suivant pour le variogramme croisé expérimental :
Supposons maintenant que nous voulons calculer la covariance et le variogramme croisé expérimental dans la direction . Qu’arrivera-t-il aux pairs de points identifiés ci-haut ?
Pour la covariance croisée expérimentale, nous allons avoir des paires de points complètement nouvelles. Nous cherchons maintenant des couples () qui sont dans la direction inverse de la précédente. Ainsi, les nouvelles paires de points sont au nombre de 4 et sont : (5.9, 2.6) ; (5.8, 2.8) ; (7.0, 3.8) ; (6.5, 4.7). Le calcul est maintenant le suivant :
[ \hat{C}{ZY,e}(1,0) = \frac{1}{N} \sum (Z_i - m_Z)(Y{i+h} - m_Y) ]
Noter que est positive tandis que est négative. Cela peut se produire avec la covariance croisée, car elle permet de capturer des asymétries.
Dans le cas du variogramme croisé expérimental, aucun changement se produit. On constate que les couples pour et sont identiques. C’est normal, car le variogramme croisé est symétrique par définition.
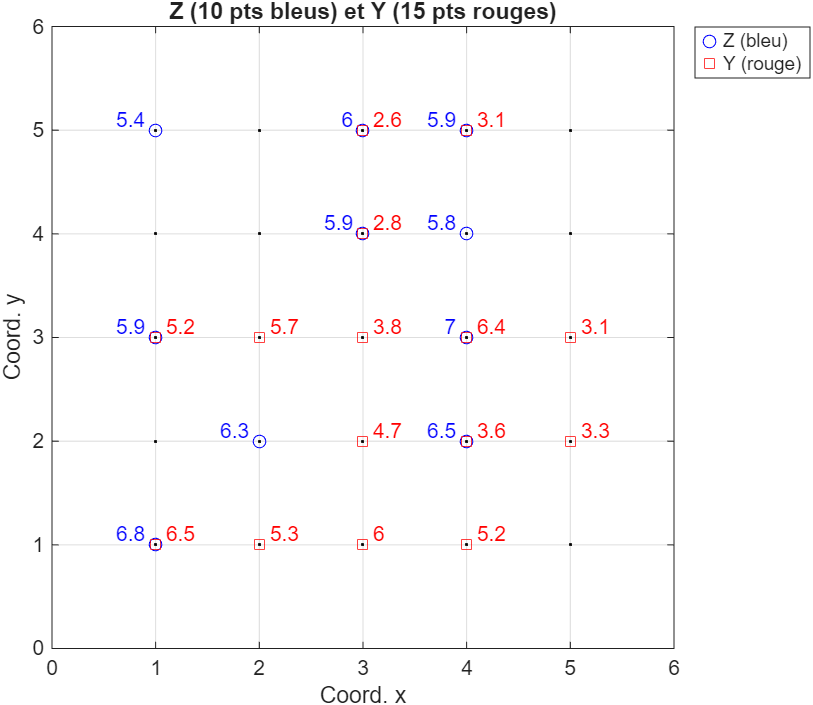
Figure 1:Exemple de données multivariables. Nuage de points des données observées et de leur corrélation.