Une étape importante avant de procéder au calcul des ressources et réserves minérales est la régularisation des données. Il s’agit d’une pratique courante dans l’estimation des ressources, considérée comme essentielle pour produire des estimations non biaisées. En général, les carottes de forages (ou le support) sont collectées sur des longueurs différentes ( ou intervalles irréguliers) en raison des variations des propriétés mécaniques des lithologies traversées, des stratégies d’échantillonnage et la sélection des supports envoyés pour analyse. En d’autres mots, nous n’analysons que rarement l’intégralité des carottes d’un forage et celles-ci n’ont pas tous la même longueur.
Une sélection est souvent réalisée afin d’envoyer uniquement les carottes jugées intéressantes pour l’analyse, introduisant ainsi un possible biais de sélection. De plus, les échantillons n’ont pas nécessairement la même longueur. Celle-ci dépend de plusieurs facteurs géomécaniques (qualité du massif rocheux) ou opérationnels (e.g., l’expérience du foreur). Il est donc fréquent d’avoir, à l’intérieur d’un même forage, des carottes de longueurs différentes.
En géostatistique, il est primordial que les échantillons aient des supports identiques (voir effet de support), c’est-à-dire que leur représentativité soit équivalente. Autrement dit, toutes les teneurs mesurées doivent correspondre à la même taille de support (par exemple, des carottes de 3 m avec densité et volume égaux). Si les supports diffèrent, il faut alors procéder à une régularisation afin d’obtenir des composites de même longueur. Ainsi, un composite est un échantillon artificiel obtenu par l’agrégation de plusieurs échantillons (ici, des carottes de forage), souvent de longueurs irrégulières pour former des segments de longueur uniforme.
Le composite est généralement calculé comme une moyenne pondérée par la longueur des échantillons, et peut également tenir compte de la densité spécifique, des changements de volume, ou du taux de récupération du carottage. La régularisation peut répondre à divers objectifs : obtenir une valeur représentative à l’intersection d’un corps minéralisé, créer des composites lithologiques ou métallurgiques, produire des composites réguliers le long des trous, par gradin ( bench an anglais), par section, par haute teneur, ou encore des composites minimaux en longueur et teneur. Chacun de ces types de composites répond à des besoins spécifiques selon les contextes d’étude. Les composites de longueur régulière ou par gradin sont les plus fréquemment utilisés pour l’estimation des ressources.
Exemple simplifié : composites réguliers¶
Considérons un trou de forage traversant un corps minéralisé où trois échantillons de longueurs différentes ont été prélevés :
Échantillon 1 : longueur = 1 m, teneur = 1.00 %
Échantillon 2 : longueur = 3 m, teneur = 5.85 %
Échantillon 3 : longueur = 2 m, teneur = 1.75 %
Sans régularisation, si l’on calcule simplement la moyenne des teneurs (sans pondération par la longueur), on obtient :
Cependant, cette valeur ne reflète pas le fait que les longueurs d’échantillons sont inégales.
Supposons maintenant que l’on veuille créer des composites de 3 mètres. Le premier composite sera formée de l’échantillon 1 (1 m) et d’une partie de l’échantillon 2 (2 m). La teneur du composite 1 sera obtenue par une moyenne pondérée par la longueur :
De même manière, le second composite sera composé d’une partie de l’échantillon 2 (1 m) et de la totalité de l’échantillon 3 (2m). La teneur du composite 2 sera aussi obtenue par une moyenne pondérée par la longueur :
Maintenant que les supports sont tous les mêmes, on peut procéder au calcul de la moyenne sans risqué d’introduire un biais, car les support sont équivalents :
On remarque ici que la moyenne régularisée est différente de la moyenne non pondérée. Cette différence illustre l’impact de la régularisation : en tenant compte des longueurs réelles des échantillons, on obtient une estimation plus représentative de la teneur présente dans le gisement.
La Fig. 1 illustre le calcul effectué ci-haut.
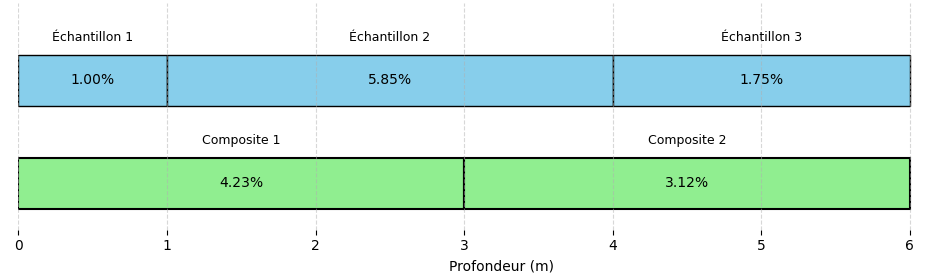
Figure 1:Exemple d’un composite.
Exemple simplifié : densité¶
Il n’y a pas que la longueur des carottes qui joue un rôle dans la régularisation des teneurs. La densité des carottes peut jouer un rôle important.
Supposons qu’un bloc de minerai de 1 mètre cube (m³) contient une teneur de 3% de cuivre. Nous voulons calculer la quantité de cuivre en fonction de la densité du minerai.
Si la densité du minerai est de 3.5 tonnes par mètre cube (t/m³), la masse totale du minerai dans 1 m³ est de 3.5 tonnes. La quantité de cuivre sera alors :
Si la densité du minerai est de 3.2 t/m³, la masse totale du minerai dans 1 m³ est de 3.2 tonnes. La quantité de cuivre sera alors :
Ainsi, pour 1 m³ de minerai avec une densité de 3.5 t/m³, la quantité de cuivre est de 105 kg, mais celle-ci chute à 96 kg lorsque la densité est de 3.2 t/m³.
Bien que la teneur en cuivre soit constante à 3%, la quantité de cuivre dans 1 m³ de minerai varie en fonction de la densité. Plus la densité est faible (3.2 t/m³ par rapport à 3.5 t/m³), moins il y a de métal dans un volume donné de minerai.
Il est alors très important de tenir compte de la densité dans l’estimation des ressources et des réserves minières. À noter que souvent, les variations de densité peuvent être considérées comme négligeables.
Importance de la régularisation¶
Bien que la régularisation ne soit pas toujours indispensable pour estimer les ressources, elle s’impose dans la majorité des cas. Elle permet d’uniformiser le support des données --- c’est-à-dire leur taille ou leur volume représenté --- et de corriger les intervalles d’échantillonnage partiels, ce qui facilite une estimation plus cohérente. La plupart des logiciels d’estimation considèrent d’ailleurs que les données sont prises sur des supports de taille constante, obligent ainsi la formation de composite.
La régularisation a aussi un effet pratique: elle dilue légèrement l’information brute, rendant les données plus comparables au niveau de sélectivité réel de l’exploitation minière. Par exemple, la hauteur des gradins en mine à ciel ouvert ou la hauteur des tranches en mine souterraine détermine souvent le niveau de détail pertinent. Il est donc courant de choisir une longueur de composite alignée avec cette sélectivité.
Le choix du jeu de données composite est crucial pour garantir la qualité et la précision du modèle de ressources. En effet, la manière dont les données sont agrégées influence directement l’estimation des ressources minérales. Plusieurs décisions clés doivent être prises lors de la création des composites afin d’assurer une modélisation robuste et fiable des ressources. Parmi ces décisions, on retrouve les questions suivantes :
Quelle est la longueur optimale des composites ?
Quel type de régularisation utiliser (longueur constante, par unité géologique ou par banc) ?
Faut-il respecter les limites géologiques lors de la régularisation ?
Comment gérer les intervalles en présence de données manquantes ?
Quelle est la longueur minimale acceptable pour un composite ?
Ces choix doivent être faits avec soin, car ils ont un impact significatif sur la qualité de l’estimation et la fiabilité du modèle géologique global.
Régularisation par trou de forage¶
Nous répondrons à ces questions à l’aide d’un exemple numérique. Dans cette lecture, nous privilégierons la méthode de régularisation par trou de forage (downhole compositing). Il est important de noter qu’il existe d’autres approches, notamment la régularisation par bancs ou par domaine géologique. Ces méthodes tiennent compte de critères de sélectivité liés aux opérations minières ou à la géologie du gisement. Cela dit, bien maîtriser la méthode par trou de forage suffit généralement à comprendre les principes fondamentaux des autres méthodes de régularisation.
Exemple numérique de régularisation par trou de forage¶
L’exemple suivant illustre un cas typique de régularisation par trou (down-the-hole), avec des échantillons dont la longueur des carottes varient entre 3 et 7 m. Certains intervalles contiennent des données manquantes, soit par perte de l’information ou non-analyse de l’échantillon. Nous appliquons une régularisation à longueur constante de 6 m et avec les hypothèses suivantes :
Longueur optimale : 6 m permet ici de réduire la variabilité sans perdre en sélectivité.
Méthode utilisée : régularisation par longueur constante en suivant la longueur du forage (down-the-hole).
Respect des limites géologiques : non pris en compte ici, mais on peut tronquer les composites à ces limites si désiré.
Gestion des données manquantes : les composites contenant des zones sans données sont conservés si la portion valide couvre au moins 50 % de la longueur nominale. Sinon, le composite est ignoré. Le seuil est fixé arbitrairement à 50 %. Ce choix peut être appuyé par une étude de corrélation entre longueur et teneur.
Exemples de calcul de composites¶
La Fig. 2 présente les résultats de la régularisation pour la distance de 60m a 90. Il y a ainsi 5 composites qui doivent etre formé (30/6=5). Nous expliquerons le calcul pour le composite 2 et 4.
Le Composite 2 couvre l’intervalle de profondeur entre 66 m et 72 m. Sa teneur est calculée comme la moyenne pondérée des teneurs selon la formule suivante :
où les longueurs et teneurs considérées correspondent uniquement aux portions valides.
Composite 4 couvre l’intervalle de 78 m à 84 m. Bien qu’il
intersecte également des carottes d’échantillonnage, la longueur totale
des portions valides dans cet intervalle est inférieure à 3 m (moins de
50 % de la longueur nominale du composite). En vertu du critère fixé, ce
composite est donc ignoré et marqué comme NaN (non défini), car il
ne respecte pas la condition minimale de validité des données. Il n’y
aura donc aucune teneur pour le composite 4.

Figure 2:Exemple complet d’une régularisation.
Choix de la longueur des composites¶
La longueur de composite choisie dans cet exemple est de 6 m. Ce choix repose d’abord sur l’analyse de la distribution des longueurs d’échantillons bruts, qui montre une concentration marquée autour de cette valeur (Fig. 3). Cela reflète une trame d’échantillonnage déjà assez régulière dans les forages.
Du point de vue géostatistique, cette régularisation à 6 m permet de réduire la variabilité locale tout en maintenant une sélectivité suffisante pour distinguer les structures géologiques majeures. Il est important de rappeler qu’une régularisation efficace cherche à augmenter le support d’échantillonnage, pas à le réduire.
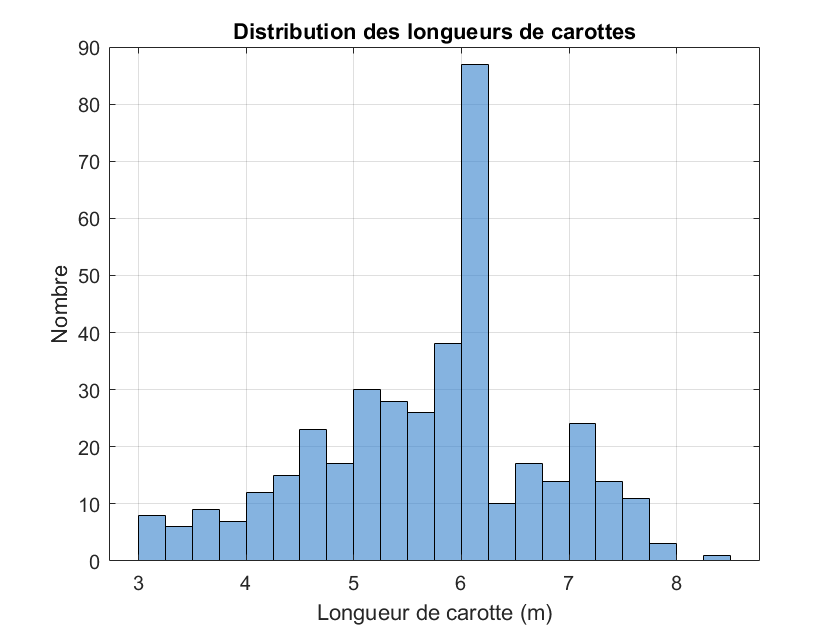
Figure 3:Histogramme des longueurs de carottes.