La dernière étapes afin d’assurer une représentativité adéquantes des teneurs est le débiaisement et le dégroupement des données. Les données de forage ne sont généralement pas collectées de manière aléatoire. Par exemple, les forages sont souvent réalisés dans des zones à forte teneur, qui sont prioritaires dans le calendrier d’exploitation. Ce biais d’échantillonnage, bien que justifié d’un point de vue opérationnel, fausse les statistiques globales. Il est donc nécessaire d’ajuster les histogrammes et les statistiques descriptives afin qu’elles soient représentatives de l’ensemble du volume d’intérêt.
Mise en contexte¶
La Fig. 1 présente les teneurs en cuivre d’un gisement synthétique suivant une distribution log-normale, de moyenne 2% et de variance unitaire. Les cercles en surbrillance indiquent la position des 140 forages. Deux zones apparaissent comme suréchantillonnées : l’une au centre de l’image, où 30 forages se concentrent dans une zone riche du gisement (cercles rouges), et une autre dans le coin inférieur gauche, où 10 forages représentent une zone de faible teneur (cercles bleus).
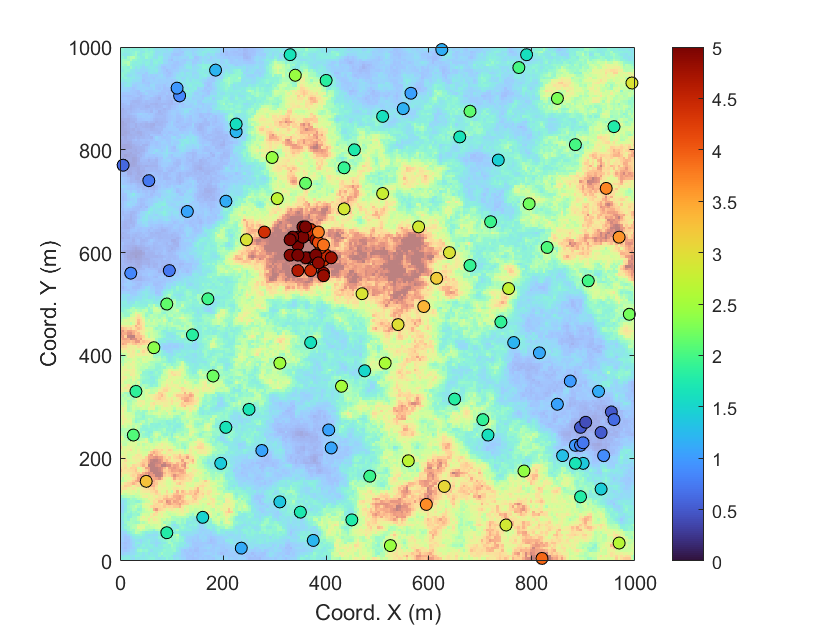
Figure 1:Teneurs en cuivre d’un gisement synthétique suivant une distribution log-normale, de moyenne 2% et de variance unitaire avec un échantillonnage ciblé.
La présence de zones de suréchantillonnage biaise le calcul de nos statistiques descriptives (par exemple, moyenne, écart-type, quantiles). Il va de soi que les 30 forages représentant une zone riche vont augmenter la teneur moyenne de nos échantillons, rendant ainsi cette moyenne non représentative de la teneur moyenne réelle du gisement. Dans cette situation, il est nécessaire de procéder au débiaisement des observations par le dégroupement de celles-ci.
La Fig. 2 présente les histogrammes normalisés — c’est-à-dire ajustés pour permettre une comparaison équitable entre les distributions — des teneurs réelles du gisement (Fig. 2a), des teneurs échantillonnées sans dégroupement (Fig. 2b) et des teneurs après dégroupement (Fig. 2c). Les statistiques descriptives sont affichées sur chaque histogramme.
La comparaison de ces statistiques permet de constater que les données brutes (figure centrale) sont fortement biaisées, en raison d’une surreprésentation des zones à haute teneur, causée par le biais d’échantillonnage. Après dégroupement, les statistiques descriptives se rapprochent nettement de celles du gisement réel : la moyenne passe de 2,60 % à 1,90 %, alors que celle du gisement est de 2,09 %. Ce rapprochement est observable pour l’ensemble des indicateurs descriptifs.
Cela illustre l’importance de corriger les biais d’échantillonnage, notamment lorsque les zones riches sont surexplorées. Dans cet exemple, l’absence de correction pourrait conduire à surestimer significativement la richesse du gisement.
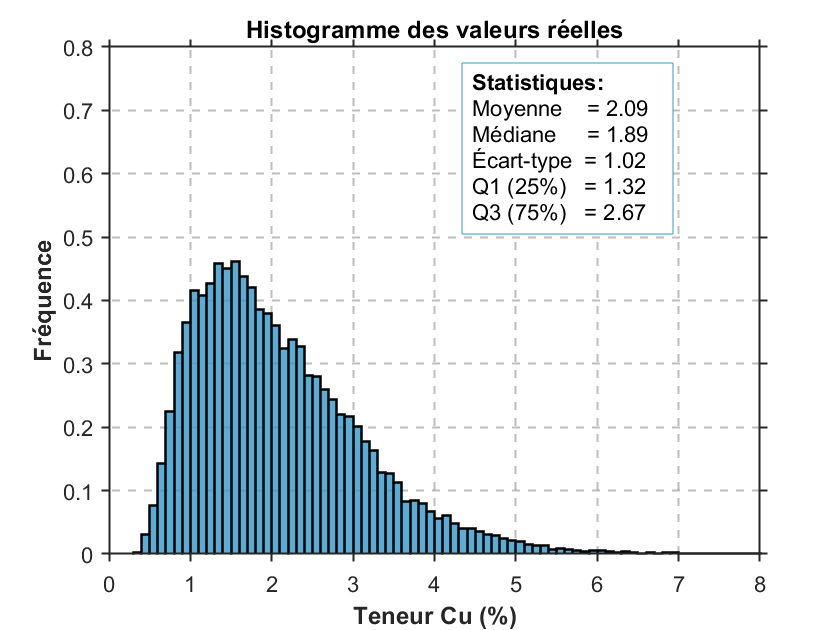
(a)Histogramme des valeurs réelles du gisement.
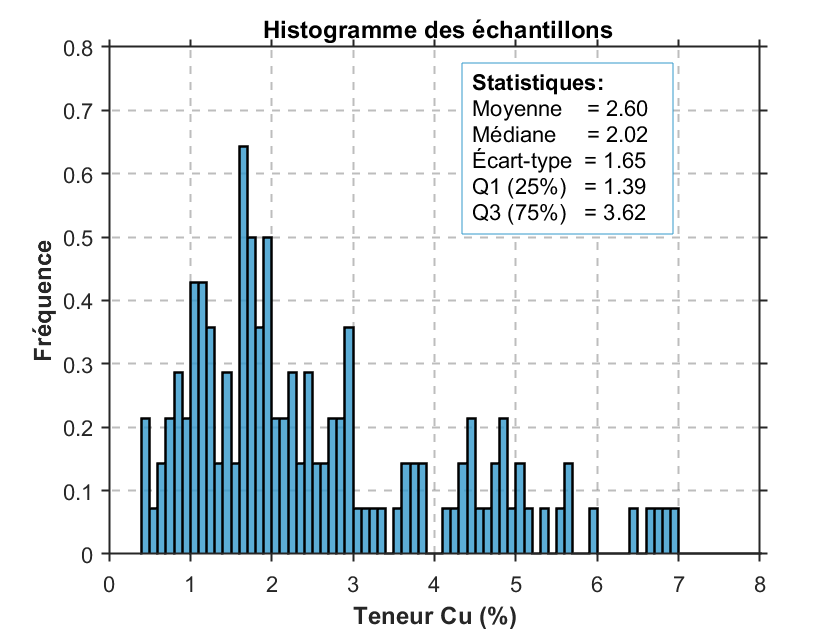
(b)Histogramme des teneurs analysées sans dégroupement.
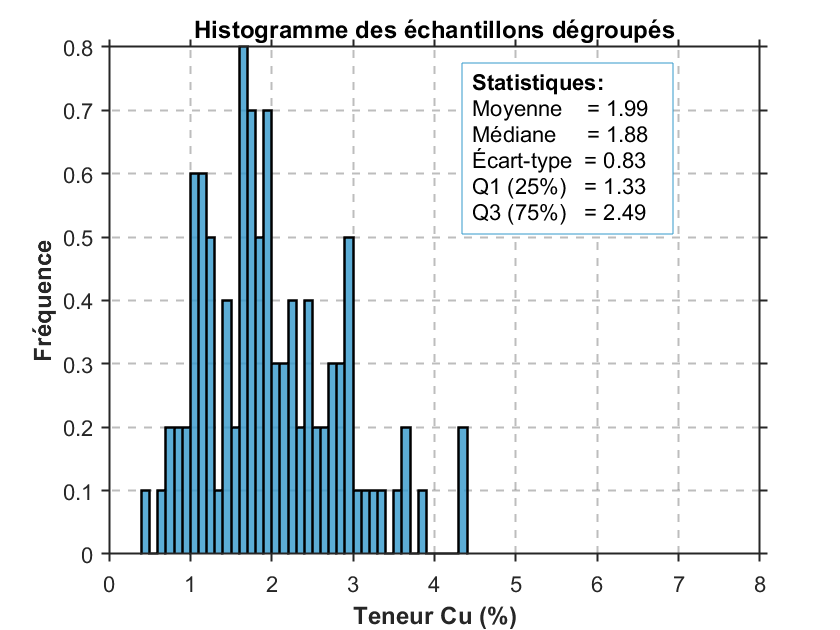
(c)Histogramme des teneurs analysées avec dégroupement.
Méthode de dégroupement¶
Les techniques de dégroupement visent à corriger les biais d’échantillonnage en attribuant un poids à chaque donnée en fonction de sa proximité avec les autres. Ces poids sont strictement positifs et leur somme est égale à 1. Les statistiques sont ensuite calculées à l’aide de ces poids pondérés.
On note plusieurs méthodes de dégroupement dans la littérature. Nous nous limiterons aux trois méthodes les plus souvent implémentée dans les logiciels de calcul de ressources et de réserves minières.
Dégroupement polygonal¶
La méthode de dégroupement polygonal est sans doute la plus simple. Elle attribue à chaque échantillon un poids proportionnel à la surface ou au volume d’influence de celui-ci. Des études ont montré que cette approche fonctionne bien lorsque les limites de la zone d’intérêt sont bien définies et que le rapport entre le plus grand et le plus petit poids est inférieur à 10 pour 1 Rossi2014.
La technique repose sur la construction de polygones d’influence autour de chaque point d’échantillonnage. Ces polygones sont définis par les médiatrices entre chaque paire de points voisins (Diagramme de Voronoï). Un exemple simple de jeu de données avec polygones d’influence est illustré à la Fig. 3
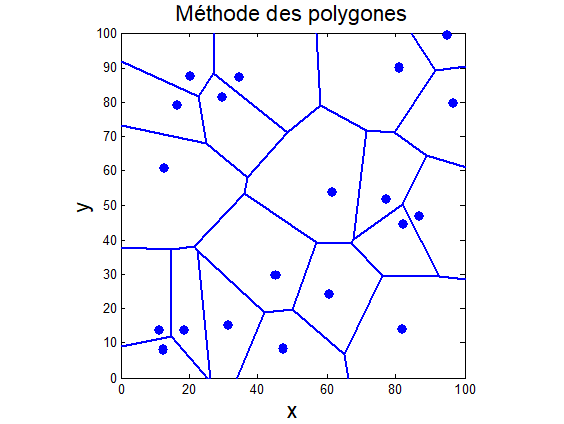
Les polygones sont obtenues par la méthode de Voronoi, un algorithme implémenté dans la grande majorité des logiciels. Nous verrons sa construction en classe. Pour chaque polygone d’influence, on calcule l’aire, puis on assigne à chaque échantillon un poids proportionnel à l’aire de son polygone par rapport à la somme totale des aires de tous les polygones, soit :
où est le poids associé à l’échantillon , est l’aire de son polygone d’influence, et est le nombre total d’échantillons.
La Fig. 4 présente 27 données de forages et les poids leurs étant associée par la méthode des polygone d’influence. On peut constater que les poids sont les plus faible au centre ou plus de données sont présente que sur les frontières ou les volumes sont plus importants.
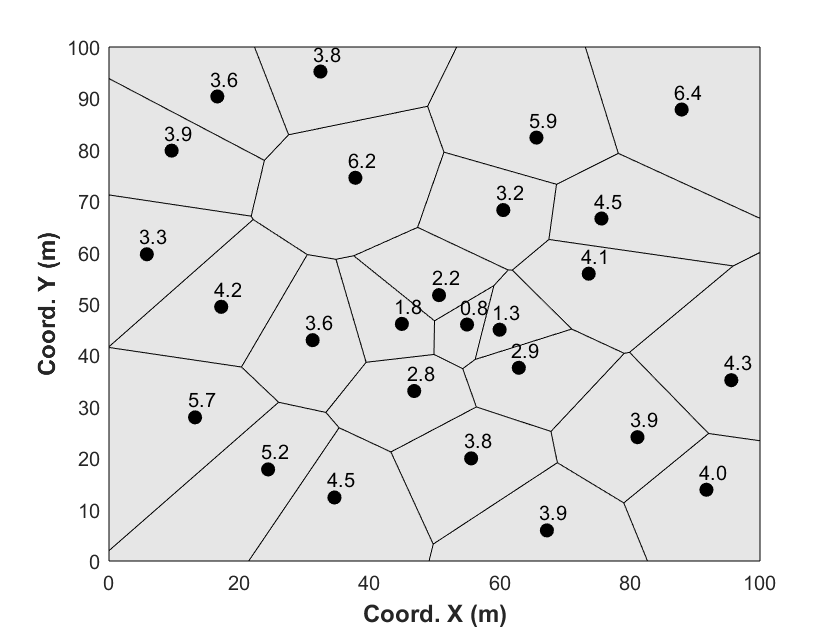
Cela constitue une grande limitation de la méthode des polygones. L’aire associée aux échantillons périphériques est en effet très sensible à la localisation de la frontière. La question de savoir comment définir correctement cette frontière est complexe, car celle-ci est rarement bien définie, surtout lorsqu’on s’éloigne du cœur du gisement. Ainsi, si la frontière est située loin des données, les échantillons périphériques se voient attribuer une quantité importante de poids, car l’aire de leurs polygones d’influence augmente. En général, cette forte sensibilité à la localisation de la limite est perçue comme une faiblesse de la méthode de dégroupement polygonal. Une technique courante consiste alors à appliquer une frontière fixe, correspondant à la zone d’intérêt. Celle-ci peut être définie par des critères géologiques, les limites de concessions, etc. Cette approche peut être pertinente selon le contexte du problème. Une autre technique consiste à attribuer une distance maximale d’influence aux échantillons, limitant ainsi leur poids en fonction de cette distance.
Dégroupement par plus proche voisin¶
La technique de dégroupement par voisin le plus proche est couramment utilisée dans l’estimation des ressources et elle est similaire à la méthode polygonale. La différence réside dans le fait qu’elle est appliquée à une grille régulière de blocs ou de nœuds de grille. À chaque bloc, le point le plus proche du jeu de données à dégrouper est attribué. Comme elle s’applique directement sur les mêmes blocs utilisés pour estimer les ressources, cette méthode est plus pratique dans le cadre de l’estimation des ressources.
La Fig. 5 présente les mêmes 27 données de forage que dans l’exemple précédent. Cette fois-ci, nous assignons directement à chaque bloc le point de forage (cercles noirs) le plus proche du centre du bloc (cercles rouges). Avec une densité de forages très régulière, la méthode de dégroupement par voisin le plus proche est pratiquement similaire à la méthode de dégroupement polygonal. L’avantage de cette approche réside dans le fait que les données sont directement associées au même support que celui utilisé pour les opérations minières et le calcul des ressources.
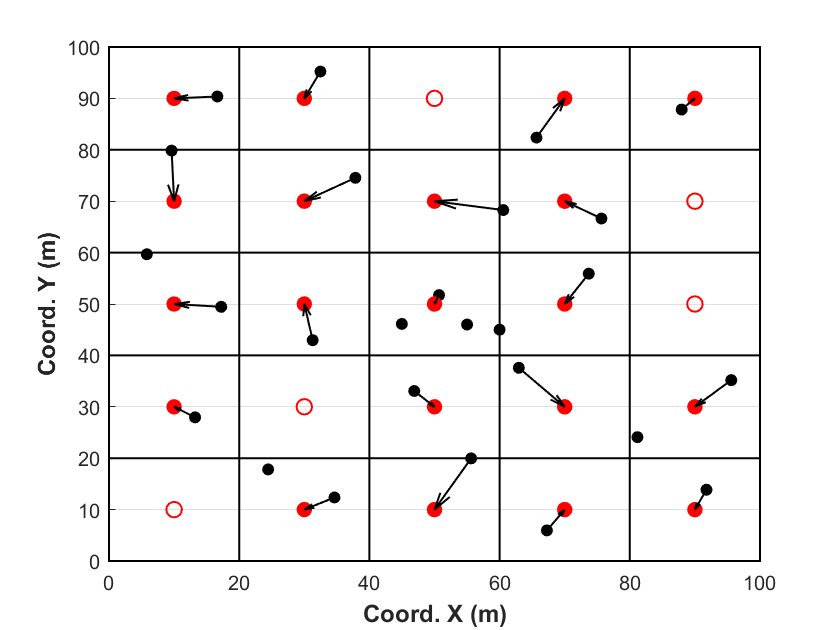
Dégroupement par cellules¶
La technique de dégroupement par cellules est une autre méthode couramment utilisée et sûrement l’une des plus populaire. Le dégroupement par cellules fonctionne comme suit :
Diviser le volume d’intérêt en une grille de cellules .
Compter les cellules occupées et le nombre de données dans chaque cellule occupée , .
Attribuer un poids à chaque donnée en fonction du nombre de données dans la même cellule. Par exemple, pour une donnée se trouvant dans la cellule , le poids de dégroupement par cellule est donné par :
Les poids sont supérieurs à zéro et leur somme est égale à un. Chaque cellule occupée se voit attribuer le même poids. Une cellule non occupée ne reçoit aucun poids.
La Fig. 6 présente les mêmes 27 données de forage que dans les deux exemples précédents. Cette fois-ci, nous comptabilisons le nombre de données situées à l’intérieur de chaque cellule (délimitées par des encadrés noirs). Pour chaque cellule, un poids provisoire est attribué à chaque point selon le principe suivant : si une seule donnée est présente dans la cellule, son poids provisoire est égal à 1 ; s’il y a deux données, chacune reçoit un poids de ; plus généralement, pour données dans une cellule, chaque point reçoit un poids provisoire de .
Une fois ces poids provisoires calculés pour l’ensemble des données, ils sont normalisés de manière à ce que leur somme soit égale à 1, en divisant chaque poids par le nombre total de cellules occupées.
On observe également que certaines cellules ne contiennent aucune donnée : dans ce cas, aucun poids n’est attribué, ce qui est représenté visuellement par un cercle rouge vide.
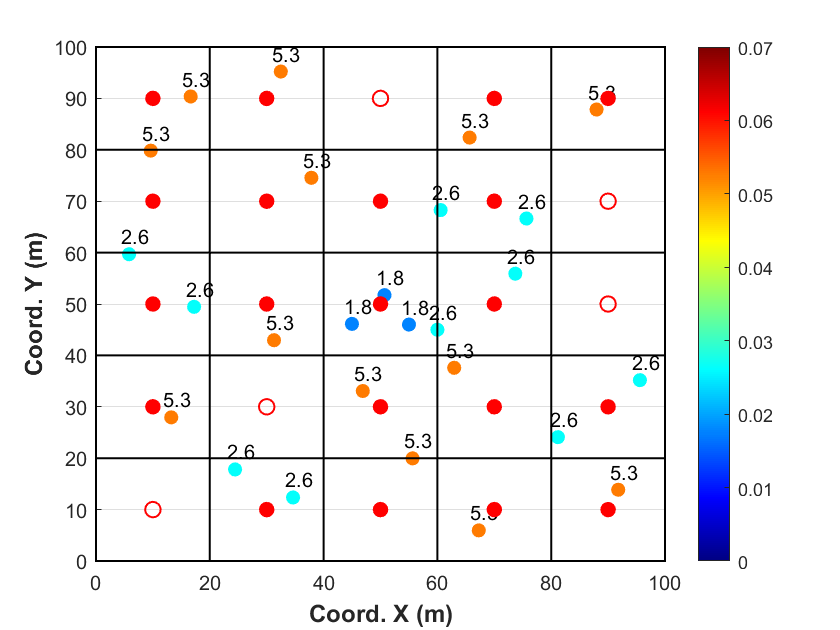
Les poids de dégroupement attribués aux données dépendent de la taille des cellules et de l’origine de la grille. Il est important de noter que cette grille n’est qu’un outil intermédiaire pour calculer des poids de dégroupement, et ne correspond pas à la grille finale utilisée pour la modélisation du gisement.
Si les cellules sont très petites, chaque donnée se retrouve dans une cellule unique, et toutes les données ont le même poids.
Si les cellules sont très grandes, toutes les données pourrait tomber dans une unique cellule et reçoivent là encore un poids égal.
Le choix de la taille, de la forme et de l’origine de la grille demande des tests de sensibilité. On cherche souvent à ajuster la taille des cellules pour obtenir environ une donnée par cellule dans les zones faiblement échantillonnées, ou à calquer la grille sur un maillage de sondages quasi-régulier s’il existe.
Il est essentiel de vérifier la sensibilité des résultats aux variations de la taille des cellules. Si une petite variation modifie fortement le résultat, c’est sans doute dû à une ou deux données avec des valeurs extrêmes mal pondérées.
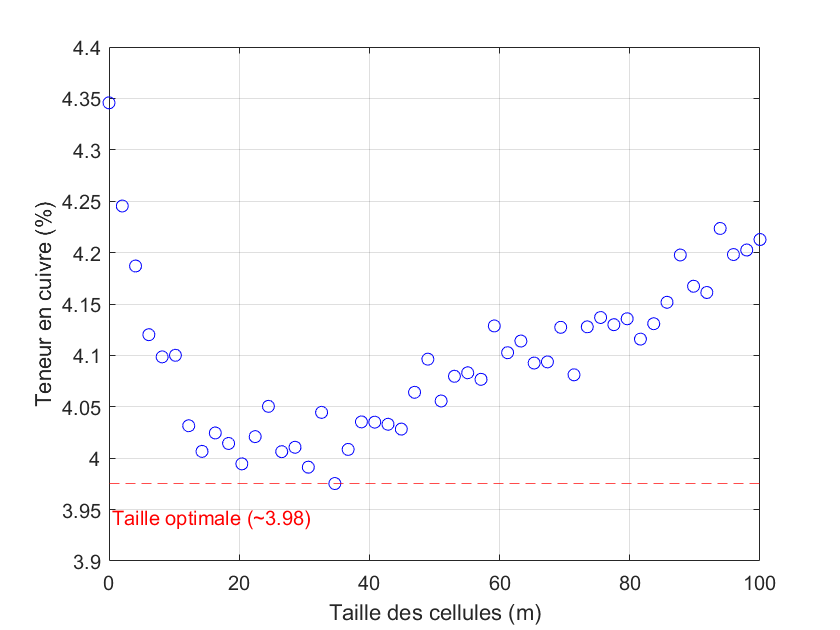
Il est aussi courant d’ajuster les poids de manière à minimiser ou maximiser la moyenne dégroupée, selon que le sur-échantillonnage se produit dans des zones à forte ou faible teneur. On peut alors tracer l’évolution de la moyenne dégroupée en fonction de la taille des cellules pour guider le choix optimal (voir Fig. 7).
Enfin, la forme des cellules doit s’adapter à la géométrie des données. Par exemple, si les données sont plus denses dans une direction (par exemple ), la taille des cellules dans cette direction doit être réduite. On appelle ce concept l’anisotropie, et il s’applique à toute méthode de déviation et de regroupement. Nous verrons en détail la notion d’anisotropie lorsque nous discuterons du variogramme.