3.4 Influence des paramètres sur la teneur optimale et le profit

La Fig. 1 illustre l’effet d’utiliser la mauvaise distribution pour déterminer la teneur de coupure optimale pour un même gisement. Supposons que les calculs ont été faits pour un ensemble de paramètres identiques sauf que l’on a considéré deux lois lognormales de variances différentes. (Paramètres utilisés : $m=1.32\$/t$ minéral ; $y=0{,}87$ ; $p=600\$/t$ métal ; $k=0$ ; $h=3.41\$/t$ minerai ; $f=11.9$ M$ ; $F=0$ M$ ; $M=12$ Mt ; $H=3.9$ Mt ; $K=0.085$ Mt). Sur la figure gauche, l’optimum est atteint à l’équilibre mine-concentrateur ( $c=0.93\%$ ) et rapporte un profit de $0.36\$/t$ minéral. Sur celle de droite, l’optimum est atteint à la teneur de coupure $0.80\%$ et un profit de $0.0.72\$/t$ minéral en résulte.

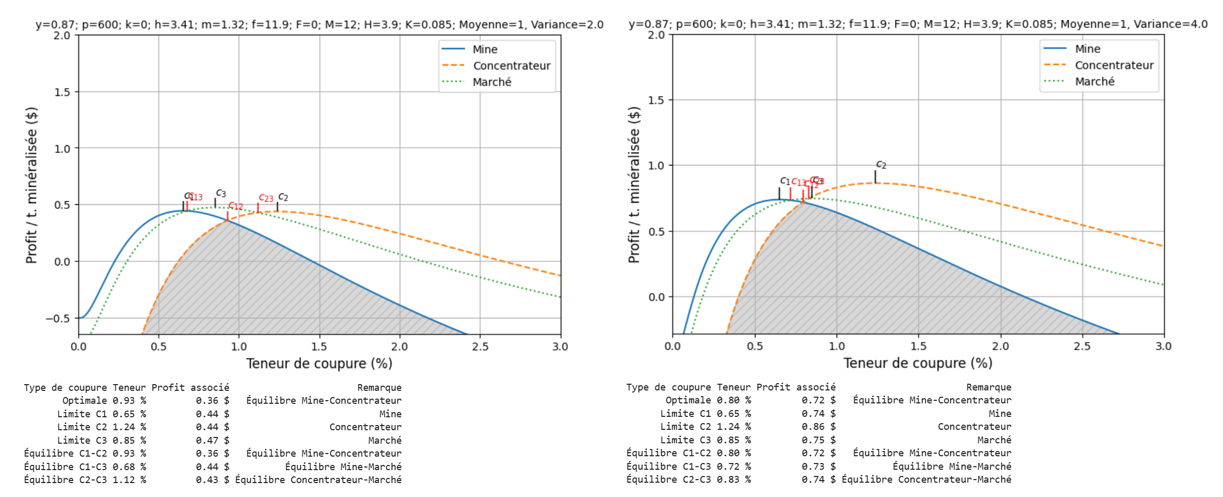
Figure 1:Impact de la variance sur le teneur de coupure.

L’exemple précédent montre combien les calculs économiques sont tributaires d’une bonne description statistique du gisement. Le gisement présente une valeur nette deux fois plus petite si $\sigma = 2%^2$ que si $\sigma = 4%^2$ . Ceci correspond à une erreur fréquente pour ce genre d’étude : on estime les teneurs de blocs par des estimateurs qui montrent une variance plus grande que les blocs réels. On prédit alors des profits irréalistes qui ne pourront se réaliser. Pour éviter les mauvaises surprises, il faut s’assurer que l’on utilise la variance des teneurs des blocs qui pourront être sélectionnés. Comme la sélection s’effectue sur des valeurs estimées, c’est en réalité la variance des valeurs estimées qu’il faut utiliser, pourvu que l’estimateur soit sans biais conditionnel. On peut montrer (voir partie géostatistique) qu’un estimateur, pour être sans biais conditionnel, doit nécessairement être moins variable que les blocs qu’il cherche à estimer. Les teneurs réelles des blocs sont elles-mêmes moins variables que les teneurs des carottes prélevées dans le gisement (effet support).

Cas simple de deux¶

Considérons le cas simple, mais courant, où le marché n’influence pas le calcul de la teneur de coupure optimale. Ainsi, nous n’avons que trois teneurs de coupure à calculer :

$c_1$ : teneur limite de la mine
$c_2$ : teneur limite du concentrateur
$c_{12}$ : teneur d’équilibre mine–concentrateur

Lorsque l’on étudie les formules permettant d’obtenir ces trois teneurs de coupure, on constate les effets suivants des différents facteurs sur les teneurs de coupure:

Facteur	$c_1$	$c_{12}$	$c_2$
Prix $(p-k)$ ↑	↓	–	↓
Coût de minage $(m)$ ↑	–	–	–
Coût de traitement $(h)$ ↑	↑	–	↑
Coût fixe $(f+F)$ ↑	–	–	↑
Taux de récupération ↑	↓	–	↓
Capacité minage $(M)$ ↑	–	↑	–
Capacité traitement $(H)$ ↑	–	↓	↓
Moyenne ↑	–	↑	–
Variance ↑	–	↓ (habituellement)	–

Cas où (c_1) est la teneur de coupure optimale¶

Si (c_1) est la t.c. optimale, alors :

[ c_{12} < c_1 < c_2 \quad \text{et} \quad c_1 < c_2 ]

Tout facteur augmentant (c_1) maintiendra (c_1) comme t.c. optimale.
Tout facteur diminuant (c_1) pourrait amener (c_{12}) à devenir la t.c. optimale.
Tout facteur diminuant (c_{12}) ne change rien.

Cas où (c_{12}) est la teneur de coupure optimale¶

Si (c_{12}) est la t.c. optimale, alors :

[ c_1 < c_{12} < c_2 \quad \text{et} \quad c_1 < c_2 ]

Tout facteur augmentant (c_1) pourrait faire de (c_1) la t.c. optimale.
Tout facteur diminuant (c_{12}) pourrait faire de (c_1) la t.c. optimale.

Cas où (c_2) est la teneur de coupure optimale¶

Si (c_2) est la t.c. optimale, alors :

[ c_1 < c_2 < c_{12} \quad \text{et} \quad c_1 < c_2 ]

Tout facteur diminuant (c_2) ne change rien.

On peut facilement observer ces phénomènes à partir de l’atelier interactif 3 — Analyse de sensibilité. Faites varier les différents paramètres et vous serez en mesure de reconstruire le tableau ci-dessus ainsi que de déduire les constats présentés dans les paragraphes précédents.