Les teneurs de coupure précédentes ont été déterminées en fonction des caractéristiques économiques et des limites de capacité de chaque composante, considérées séparément. On peut également définir trois autres teneurs de coupure, qui feront intervenir la dépendance entre les différentes capacités de la minière. Ces teneurs, dites d’équilibre, sont définies de manière à ce que les éléments pris deux à deux soient en équilibre en termes de quantités traitées.
Autrement dit, on cherche à déterminer la teneur de coupure de sorte que, par exemple, la mine et le concentrateur opèrent tous deux à pleine capacité. Trois scénarios d’équilibre sont alors distingués : (1) la mine est en équilibre avec le concentrateur, (2) la mine est en équilibre avec le marché, et (3) le concentrateur est en équilibre avec le marché.
Teneur de coupure d’équilibre : Mine-Concentrateur¶
La teneur de coupure d’équilibre entre la mine et le concentrateur est choisie de sorte que la quantité totale de matériau minéralisé extrait par la mine puisse être entièrement traitée au concentrateur, lequel a une capacité de tonnes de minerai. Ainsi, la relation suivante doit être satisfaite :
Cela signifie que la teneur de coupure permet de sélectionner suffisamment de tonnes de matériau minéralisé pour faire fonctionner le concentrateur à pleine capacité. La teneur de coupure est donc déterminée de manière à équilibrer cette équation. Il est donc nécessaire de connaître la distribution statistique des teneurs du gisement afin de déterminer la valeur de correspondant à une teneur de coupure donnée . La teneur de coupure qui permet d’établir l’égalité dans l’équation est appelée teneur de coupure d’équilibre mine-concentrateur, notée .
Nous verrons dans une prochaine section comment construire la courbe en fonction de . Celle-ci dépendra de la distribution statistique du gisement.
Teneur de coupure d’équilibre : Mine-Marché¶
De manière analogue, la teneur de coupure d’équilibre entre la mine et le marché est déterminée afin d’assurer que toutes les tonnes de matériau minéralisé extraites soient vendues sur le marché, dont la capacité est de tonnes de métal. Il s’agit donc d’identifier la teneur de coupure qui satisfait la relation suivante :
Cette relation implique qu’il faut miner tonnes de matériau minéralisé pour répondre à la demande du marché. Cette teneur de coupure est appelée teneur de coupure d’équilibre mine-marché, notée .
Teneur de coupure d’équilibre : Concentrateur-Marché¶
Enfin, la teneur de coupure d’équilibre entre le concentrateur et le marché est déterminée afin d’assurer que la totalité des tonnes de minerai traitées soient transformées en métal pouvant être vendues sur le marché de capacité . On cherche ainsi la teneur de coupure qui satisfait l’équation suivante :
. Cette relation montre qu’il faut avoir tonnes de minerai pour répondre à la demande du marché. Cette teneur de coupure est appelée teneur de coupure d’équilibre concentrateur-marché, notée .
Distribution des teneurs¶
Pour être en mesure de déterminer les teneurs de coupure d’équilibre, il est impératif de connaître la distribution des teneurs du gisement. À partir de cette distribution, il est possible de tracer les courbes de en fonction de et de en fonction de , afin de déterminer les trois teneurs de coupure qui satisfont les relations d’équilibre présentées précédemment.
Nous supposerons que nous sommes en mesure d’obtenir, dans les règles de l’art, la distribution statistique de notre gisement. Dans le cadre de ce cours, nous supposerons que la distribution statistique des teneurs suit une loi log-normale. Il sera alors possible, une fois cette distribution estimée par des méthodes géostatistiques, de construire les courbes nécessaires à la résolution du problème.
Rappel de probabilité et statistique¶
Soit une variable aléatoire qui suit une loi normale de moyenne et de variance , on note que . En procédant au centrage et à la réduction de la variable , on peut transformer celle-ci en une loi normale de moyenne nulle et de variance unitaire par : . Ainsi, une table unique de la loi suffit pour calculer les probabilités de toute loi normale.
La fonction de densité de probabilité de la loi normale est donnée par :
et sa fonction de répartition (ou fonction de distribution cumulative) est donnée par :
Maintenant, supposons que notre variable aléatoire suit une loi log-normale avec moyenne et variance . Cela signifie que .
Le lien entre et est donné par les relations suivantes :
Il est donc possible de déterminer les paramètres d’une loi normale à partir des paramètres d’une loi log-normale.
Construction des courbes¶
Sachant qu’une teneur de coupure agit comme un seuil, on peut définir , soit la proportion de minerai sélectionné, à partir de la fonction de répartition de la distribution étudiée :
où est la fonction de densité de la variable aléatoire . Supposons que suit une loi log-normale de moyenne et de variance . On peut alors transformer cette distribution en loi normale à l’aide des équations précédentes, ce qui permet d’obtenir la relation suivante :
où désigne la fonction de répartition de la loi normale standard. Ainsi, à partir d’une table de la loi normale, ou plus simplement à l’aide d’un outil numérique, on peut calculer la valeur de pour toute valeur de .
Maintenant, la valeur , qui représente la teneur moyenne du minerai sélectionné, est donnée par la relation suivante :
Sans entrer dans les détails de la démonstration, cette moyenne peut être calculée à l’aide de la formule suivante :
Ce qu’il faut retenir ici, c’est que lorsque la moyenne et la variance de la distribution des teneurs (supposée log-normale, ce qui est fréquemment le cas en pratique) sont connues, il devient possible de calculer les variables et en fonction de la teneur de coupure .
Exemples numérique¶
La distribution des teneurs en cuivre (Cu) d’un gisement suit une loi log-normale avec une moyenne et la variance est de . Nous souhaitons calculer les valeurs de et pour une teneur de coupure .
1. Calcul de ¶
La teneur de coupure est donnée par . L’écart-type de la loi normale associée à la loi log-normale est calculé comme suit :
Ensuite, la fonction de répartition de la loi normale standard est utilisée pour calculer , qui est donné par :
2. Calcul de ¶
La teneur moyenne , qui représente la teneur moyenne des minerais sélectionnés, est donnée par la formule suivante :
3. Calcul à partir de la Table de la loi normale¶
La Table de la Loi Normale fournit des valeurs de la fonction de répartition pour des valeurs de qui suivent une loi normale , c’est-à-dire une loi normale de moyenne 0 et de variance 1.
Cependant, la table est généralement construite pour des valeurs de positives, car la fonction de répartition d’une loi normale est symétrique par rapport à 0. En effet, si suit une loi normale de moyenne 0 et de variance 1, et si est négatif, on peut exploiter cette symétrie pour déterminer . Ainsi, pour un négatif, il suffit d’utiliser la relation suivante :
Cela permet de calculer la probabilité qu’une valeur de soit inférieure à un certain seuil même si ce seuil est négatif. Par exemple, pour , on peut chercher la valeur de dans la table et utiliser la relation .
Pour obtenir la probabilité que soit inférieur à une certaine valeur, il suffit de chercher la valeur de dans la table et de lire la probabilité correspondante. Par exemple, si , on peut lire directement . Pour , on utilise la relation .
La table de la loi normale est fournie en fin de section.
Exemple du calcul des teneurs d’équilibre¶
Pour calculer les teneurs d’équilibre, on vous fournira généralement les courbes , et en fonction de , comme illustré à la Fig. 1, ou bien il faudra les calculer comme présenté dans la section précédente.
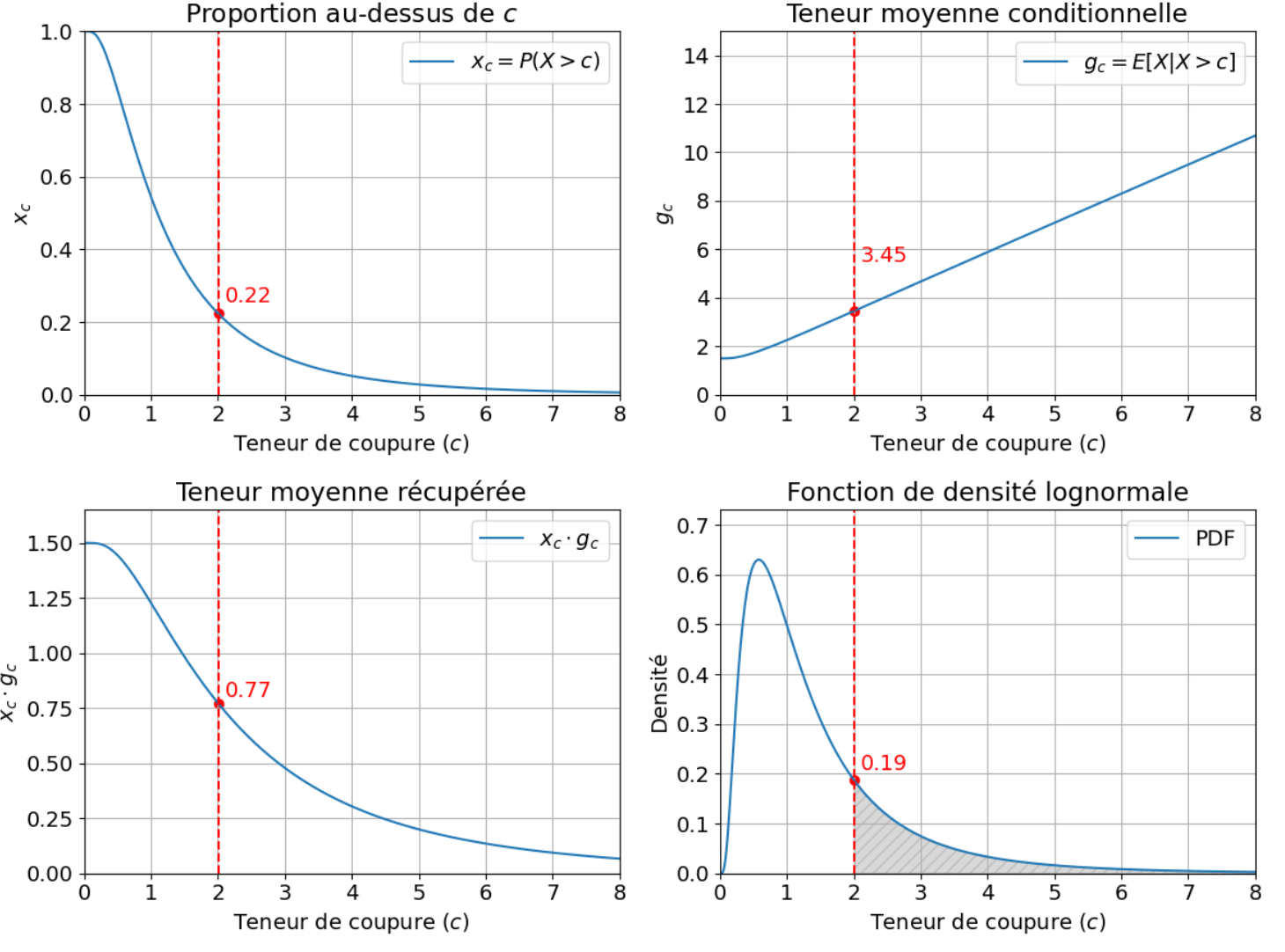
Figure 1:Courbes , et calculées numériquement.
Par exemple, pour la teneur de coupure d’équilibre mine–concentrateur , si la capacité de minage est de 10 et que la capacité de traitement est de 2,2, on doit obtenir :
Si la moyenne () et la variance () de la distribution log-normal sont respectivement de et , on peut alors construire les courbes de la Fig. 1. Par lecture graphique, on obtient que la teneur de coupure correspondante est d’environ .
On peut déduire la teneur de coupure d’équilibre mine-marché et concentrateur-marché de la même manière, à partir de la lecture graphique.