La géostatistique est une branche des statistiques dédiée à l’analyse des données spatiales et spatio-temporelles. Elle permet notamment de modéliser et de prédire les distributions de probabilité de variables telles que les teneurs en minerai. Pour bien en saisir les principes, il est essentiel de maîtriser la terminologie et les concepts fondamentaux des probabilités et des statistiques.
Variable aléatoire, fonction de densité et fonction de répartition¶
Une variable aléatoire (v.a.) est une fonction mathématique qui associe un résultat numérique à chaque issue possible d’une expérience aléatoire. Bien que les valeurs possibles de la v.a. soient connues, sa réalisation précise ne peut être déterminée a priori sans observation directe. Par exemple : la teneur en cuivre d’une carotte de forage de 1 mètre, l’épaisseur d’une veine minéralisée, la concentration d’un polluant dans une nappe phréatique ou le pH de l’eau de pluie.
Même si la valeur exacte que prendra une v.a. n’est pas connue, il est possible d’estimer la probabilité qu’elle prenne certaines valeurs.
Cette information est décrite à l’aide de la fonction de masse pour les v.a. discrètes et de la fonction de densité , pour les v.a. continues. Dans le cadre du cours, nous nous concentrerons sur les v.a. continues.
La fonction de densité vérifie deux propriétés essentielles :
Elle est positive partout :
L’aire sous la courbe est égale à 1 (probabilité totale) :
La probabilité que la v.a. prenne une valeur comprise entre deux bornes et , soit , est donnée par l’intégrale de la fonction de densité entre ces deux bornes :
Cela mène à la définition de la fonction de répartition, notée , qui représente la probabilité que la v.a. prenne une valeur inférieure ou égale à :
La fonction de répartition est une fonction croissante, bornée entre 0 et 1, et continue pour les variables continues. Elle est particulièrement utile pour visualiser la distribution cumulative des probabilités et pour déterminer des quantiles, comme la médiane (valeur pour laquelle ).
Lien avec la géostatistique¶
Soit une v.a. représentant la valeur d’intérêt (comme une teneur, une température, ou un niveau piézométrique) à une position spatiale . Bien qu’une valeur réelle existe à ce point, la géostatistique considère cette valeur comme aléatoire tant qu’elle n’a pas été mesurée. Ainsi, à partir des informations disponibles, on définit la probabilité que cette valeur prenne une certaine plage de valeurs, via la fonction de répartition conditionnelle :
Cette formulation met en lumière que, en géostatistique, la fonction de répartition dépend explicitement de la localisation de la variable. Cela souligne le caractère régionalisé des variables aléatoires étudiées, c’est-à-dire leur dépendance à une position spatiale ou temporelle.
Mesures de tendance centrale¶
Les mesures de tendance centrale résument une distribution de probabilité par une valeur représentative des résultats possibles. Voici les principales :
Mode : valeur pour laquelle la fonction de densité est maximale. Il s’agit du point le plus probable :
Médiane : valeur telle que la moitié des observations se situent en dessous de cette valeur :
Moyenne (ou espérance) : valeur moyenne attendue de la variable aléatoire, notée :
Ces mesures peuvent différer selon la forme de la distribution. Par exemple, pour une distribution symétrique comme la loi normale, la moyenne, la médiane et le mode coïncident. Pour des distributions asymétriques (ex. : loi log-normale), ces mesures seront différentes. La Fig. 1 présente ce phénomène.
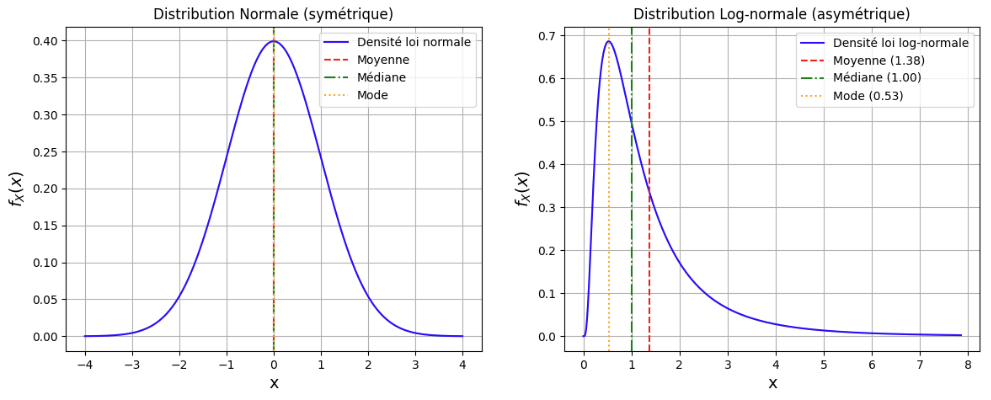
Figure 1:Illustration des principales mesures de tendance centrale (mode, médiane et moyenne) sur deux distributions de probabilité : une loi normale symétrique (gauche) où ces mesures coïncident, et une loi log-normale asymétrique (droite) où elles diffèrent. Les zones en couleur représentent les aires cumulées correspondant à la médiane.
Mesures de dispersion¶
Les mesures de dispersion décrivent la variabilité ou l’étendue des valeurs d’une variable aléatoire autour de sa moyenne. Elles sont essentielles pour comprendre l’incertitude et la répartition des données.
Variance : Mesure l’étendue des valeurs par rapport à la moyenne, quantifiant l’écart quadratique moyen :
Écart-type : La racine carrée de la variance, exprimant la dispersion des données dans les mêmes unités que la variable, pour une interprétation plus intuitive :
Asymétrie : Indique l’asymétrie de la distribution par rapport à sa moyenne. Une asymétrie positive signifie une queue plus longue vers la droite, négative vers la gauche :
Aplatissement : Mesure le degré de “pic” ou de “plat” de la distribution par rapport à une distribution normale. Une valeur élevée indique une distribution plus pointue avec des queues plus épaisses :
La Fig. 2 présente ces mesures de dispersion sur une loi normale et pour une loi log-normale.
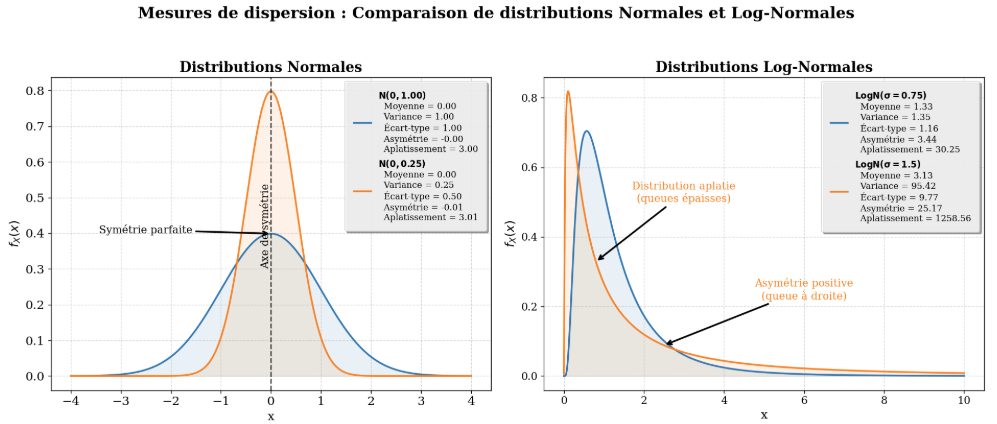
Figure 2:Comparaison des mesures de dispersion pour deux distributions de probabilité. La distribution normale (gauche) est symétrique avec une faible asymétrie et un aplatissement proche de 3 (valeur normale). La distribution log-normale (droite) est asymétrique avec une forte queue à droite, illustrant une asymétrie positive et un aplatissement plus élevé, indiquant une distribution plus pointue et avec des queues épaisses.
Estimation à partir d’un échantillon¶
L’estimation à partir d’un échantillon consiste à inférer les caractéristiques d’une population ou d’une distribution inconnue à partir de données observées. Ces estimations, basées sur des statistiques calculées à partir de l’échantillon, incluent les paramètres de tendance centrale, de dispersion, et la forme de la distribution de la variable.
Moyenne empirique : L’estimation de la moyenne de la population à partir d’un échantillon est donnée par la somme des valeurs observées divisée par leur nombre total :
Elle est l’estimateur de la tendance centrale de la variable aléatoire.
Variance empirique : Pour estimer la variabilité des données d’un échantillon par rapport à la moyenne empirique, on utilise :
Le facteur (au lieu de ) est une correction pour obtenir un estimateur sans biais de la variance de la population.
Fonction de densité : La forme de la fonction de densité peut être visualisée et estimée à l’aide d’un histogramme, qui représente la distribution des données par intervalles.
Fonction de répartition empirique : Notée , elle donne la proportion d’observations inférieures ou égales à une valeur donnée dans l’échantillon :
Elle permet de visualiser la distribution cumulative des données.
Estimateur sans biais : Un estimateur est dit sans biais si son espérance mathématique est égale à la valeur réelle du paramètre qu’il estime. Autrement dit, en moyenne, un estimateur sans biais fournit une estimation correcte du paramètre cible. Par exemple, l’estimateur d’une teneur vraie est sans biais si :
Fonction de densité conjointe¶
Lorsqu’on considère plusieurs variables aléatoires, comme deux variables et , leur dépendance peut être représentée par une fonction de densité conjointe, notée . Cette fonction décrit la probabilité conjointe que prenne la valeur et prenne la valeur simultanément.
La condition de normalisation de cette fonction est la suivante :
Dans le cas de deux variables aléatoires, les mesures usuelles de dépendance sont la covariance et la corrélation :
Covariance :
Corrélation :
La corrélation est une normalisation de la covariance, ce qui permet d’obtenir une plage de valeurs comprises entre . Une valeur de 1 indique une dépendance linéaire positive parfaite, signifiant que et varient linéairement dans la même direction. Une valeur de -1 signifie une dépendance linéaire négative parfaite (quand augmente, diminue de manière parfaitement linéaire). Une valeur de 0 indique l’absence de dépendance linéaire entre et . Il est crucial de noter que si et sont indépendantes, alors leur covariance (et donc leur corrélation) est nulle ; cependant, l’inverse n’est pas toujours vrai (une corrélation nulle n’implique pas nécessairement l’indépendance, sauf dans des cas spécifiques comme la loi normale). La Fig. 3 montre différents scénarios de corrélation entre deux variables.
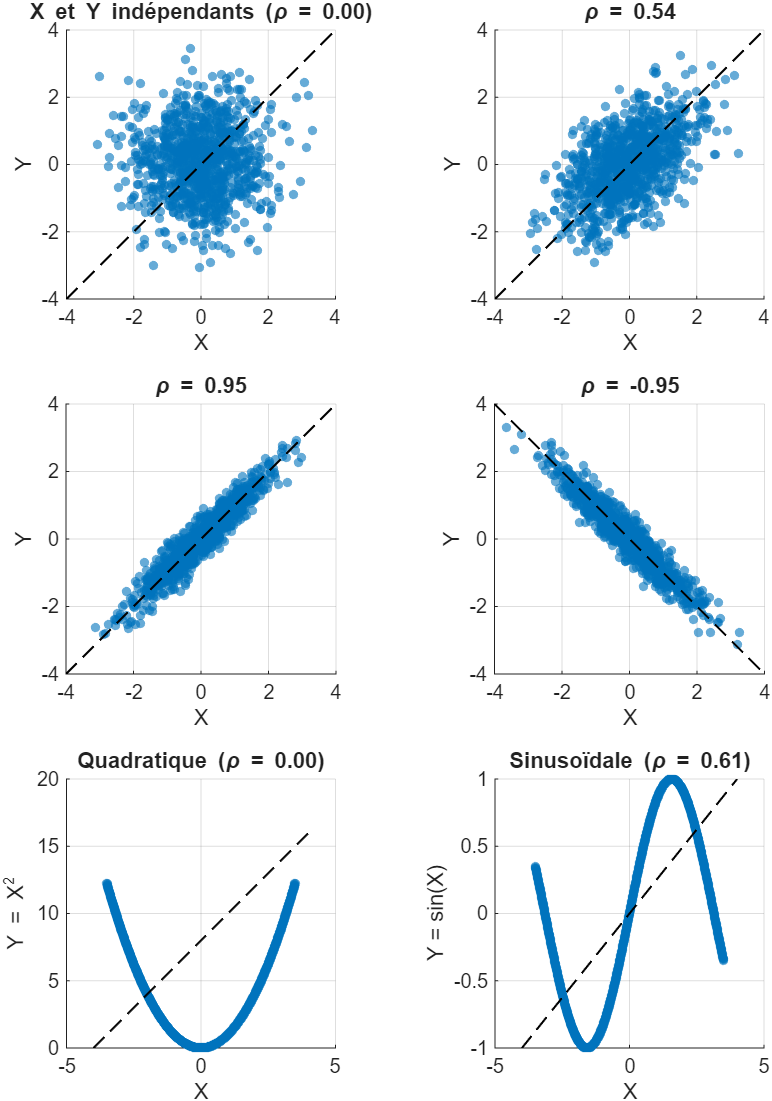
Figure 3:Différentes corrélations entre deux variables aléatoires et .
Il est également important de noter que si et sont indépendantes, alors la covariance entre et est nulle, c’est-à-dire :
Propriétés¶
La variance de la somme de deux variables aléatoires et est donnée par :
De plus, la variance d’une combinaison linéaire de et est donnée par :
Enfin, la variance de la somme pondérée de variables aléatoires est donnée par :
Ces relations sont fondamentales en géostatistique. Leur maîtrise est essentielle, car elles permettent de quantifier et de modéliser la dépendance entre variables, ce qui est crucial pour l’analyse et la prédiction des valeurs à des localisations non échantillonnées dans les contextes miniers de ce cours.